Auto involutivo Immagini Stock
(4)Filtri rapidi:
Auto involutivo Immagini Stock
Accessori medicali per l'introduzione del fluido nel retto Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-accessori-medicali-per-l-introduzione-del-fluido-nel-retto-132534336.htmlRMHKHCW4–Accessori medicali per l'introduzione del fluido nel retto
. I principi della geometria proiettiva applicati alla linea retta e alla forma conica di un triangolo auto-polare, se viene dato un vertice, è la tangentedda quel punto al cerchio. Se i due punti coniugati (che vertici dell'arco) sono aecollineari con il centro del cerchio, uno dei vertici del triangolo è atinfinito e due lati sono paralleli. Ogni triangolo autoconiugato rispetto al cerchio di punta deve essere ottuso ansled. 140 principi degli ESEMPI di Geontetrij proiettivi. (1) se da un punto tixcd si tracciano perpendicolari alle coppie di coniugati di una matita in involuzione, le linee jo Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/i-principi-della-geometria-proiettiva-applicati-alla-linea-retta-e-alla-forma-conica-di-un-triangolo-auto-polare-se-viene-dato-un-vertice-e-la-tangentedda-quel-punto-al-cerchio-se-i-due-punti-coniugati-che-vertici-dell-arco-sono-aecollineari-con-il-centro-del-cerchio-uno-dei-vertici-del-triangolo-e-atinfinito-e-due-lati-sono-paralleli-ogni-triangolo-autoconiugato-rispetto-al-cerchio-di-punta-deve-essere-ottuso-ansled-140-principi-degli-esempi-di-geontetrij-proiettivi-1-se-da-un-punto-tixcd-si-tracciano-perpendicolari-alle-coppie-di-coniugati-di-una-matita-in-involuzione-le-linee-jo-image372455372.htmlRM2CHXPHG–. I principi della geometria proiettiva applicati alla linea retta e alla forma conica di un triangolo auto-polare, se viene dato un vertice, è la tangentedda quel punto al cerchio. Se i due punti coniugati (che vertici dell'arco) sono aecollineari con il centro del cerchio, uno dei vertici del triangolo è atinfinito e due lati sono paralleli. Ogni triangolo autoconiugato rispetto al cerchio di punta deve essere ottuso ansled. 140 principi degli ESEMPI di Geontetrij proiettivi. (1) se da un punto tixcd si tracciano perpendicolari alle coppie di coniugati di una matita in involuzione, le linee jo
. I principi di geometria proiettiva applicati alla linea retta e agli oint conici degli intervalli sono a, a, b, b. Sia r e t le linee ah. aband ab. ab. Lasciate che le tangenti da rt al cerchio o conico siano i e m. Elementi auto-corrispondenti 237 allora poiché L e M sono i doppi punti dell'involuzione sul cerchio o conico (Art 75), sland SM sono i doppi raggi della matita di involuzione. (ii) prendere qualsiasi cerchio e lasciare che la tangente di sany a questo cerchio tagli la involuzione in AABB. Costruire sul lato destro di (i) i doppi elementi Land M di questo intervallo di involuzione. I raggi che uniscono questi punti Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/i-principi-di-geometria-proiettiva-applicati-alla-linea-retta-e-agli-oint-conici-degli-intervalli-sono-a-a-b-b-sia-r-e-t-le-linee-ah-aband-ab-ab-lasciate-che-le-tangenti-da-rt-al-cerchio-o-conico-siano-i-e-m-elementi-auto-corrispondenti-237-allora-poiche-l-e-m-sono-i-doppi-punti-dell-involuzione-sul-cerchio-o-conico-art-75-sland-sm-sono-i-doppi-raggi-della-matita-di-involuzione-ii-prendere-qualsiasi-cerchio-e-lasciare-che-la-tangente-di-sany-a-questo-cerchio-tagli-la-involuzione-in-aabb-costruire-sul-lato-destro-di-i-i-doppi-elementi-land-m-di-questo-intervallo-di-involuzione-i-raggi-che-uniscono-questi-punti-image372373953.htmlRM2CHR2NN–. I principi di geometria proiettiva applicati alla linea retta e agli oint conici degli intervalli sono a, a, b, b. Sia r e t le linee ah. aband ab. ab. Lasciate che le tangenti da rt al cerchio o conico siano i e m. Elementi auto-corrispondenti 237 allora poiché L e M sono i doppi punti dell'involuzione sul cerchio o conico (Art 75), sland SM sono i doppi raggi della matita di involuzione. (ii) prendere qualsiasi cerchio e lasciare che la tangente di sany a questo cerchio tagli la involuzione in AABB. Costruire sul lato destro di (i) i doppi elementi Land M di questo intervallo di involuzione. I raggi che uniscono questi punti
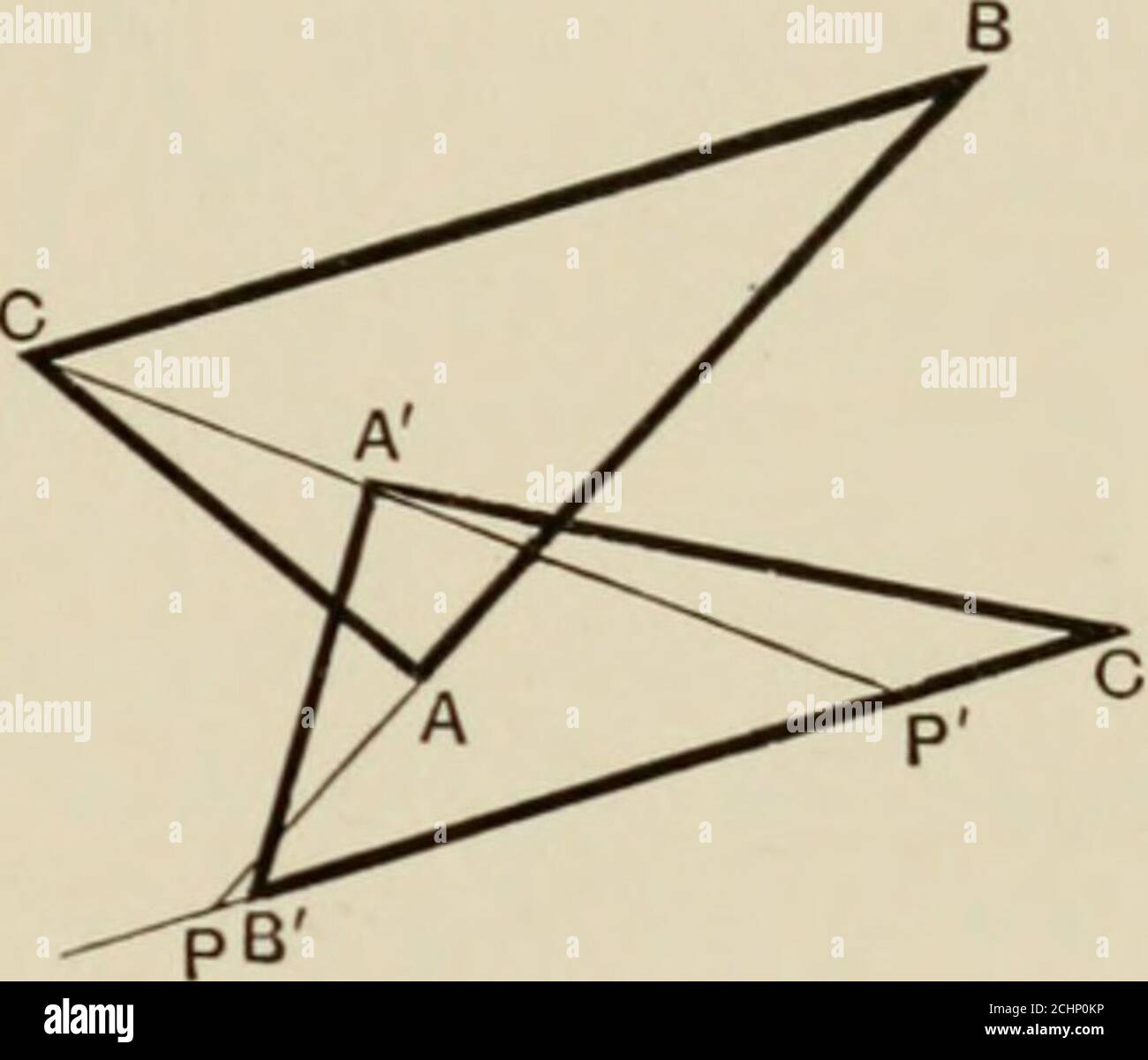. I principi della geometria proiettiva applicati alla linea retta e ai coniugi conici di ^j^i e A«Bo, cioè i doppiamente elementi dell'involuzione che essi determinano. Teoremi relativi a due conie 269 (Art 48) nel caso (1) questi punti sono reali, (2) questi punti sono punti immaginari coniugati, (3) questi punti sono reali, „ (4) questi punti sono reali. „ nel caso (2) le conie si intersecano in due punti reali e in due punti immaginari. Due conie ivhich intersecano in quattro punti distinti possono avere solo un triangolo autoconiugato con onecomcon. Se possibile, ABC e ABC siano due comuni autoconiugatetriangoli. Th Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/i-principi-della-geometria-proiettiva-applicati-alla-linea-retta-e-ai-coniugi-conici-di-j-i-e-a-bo-cioe-i-doppiamente-elementi-dell-involuzione-che-essi-determinano-teoremi-relativi-a-due-conie-269-art-48-nel-caso-1-questi-punti-sono-reali-2-questi-punti-sono-punti-immaginari-coniugati-3-questi-punti-sono-reali-4-questi-punti-sono-reali-nel-caso-2-le-conie-si-intersecano-in-due-punti-reali-e-in-due-punti-immaginari-due-conie-ivhich-intersecano-in-quattro-punti-distinti-possono-avere-solo-un-triangolo-autoconiugato-con-onecomcon-se-possibile-abc-e-abc-siano-due-comuni-autoconiugatetriangoli-th-image372350378.htmlRM2CHP0KP–. I principi della geometria proiettiva applicati alla linea retta e ai coniugi conici di ^j^i e A«Bo, cioè i doppiamente elementi dell'involuzione che essi determinano. Teoremi relativi a due conie 269 (Art 48) nel caso (1) questi punti sono reali, (2) questi punti sono punti immaginari coniugati, (3) questi punti sono reali, „ (4) questi punti sono reali. „ nel caso (2) le conie si intersecano in due punti reali e in due punti immaginari. Due conie ivhich intersecano in quattro punti distinti possono avere solo un triangolo autoconiugato con onecomcon. Se possibile, ABC e ABC siano due comuni autoconiugatetriangoli. Th
