Alamy logo

Equazione parametrica Immagini Stock

(17)
Filtri rapidi:

Equazione parametrica Immagini Stock

Figura di Lissajous, artwork Foto Stock
RFD1P2W0–Figura di Lissajous, artwork
Collezioni varie Smithsonian . ). 2.417 equazione polare dell'ellisse, r = FP, 6 = angolo . XFP, a(j -e^) i - e cos d2.418 r = 0P, d = angolo XOP, VI - e^ cos^ 6 2.419 equazione di Ellipse in termini di p, perpendicolare da F sul thetangent a P, e r, il vettore di raggio FP: 1 = f Lp^ r a i == retto semiclatus. 2.420 Iperbole (Fig. S). 2.421 o, Centro; F, F, Foci.equazione di iperbole, origine a o, ^ y- a2 62 ^ X = OM, y = MP, a = OA= OA. 2.423 equazioni parametriche di hperbola, X = a sec <f), y = b tan 0. </) = angolo XOP, dove P è il punto in cui l'ordinata a T incontra Foto Stock
RM2AWRDGT–Collezioni varie Smithsonian . ). 2.417 equazione polare dell'ellisse, r = FP, 6 = angolo . XFP, a(j -e^) i - e cos d2.418 r = 0P, d = angolo XOP, VI - e^ cos^ 6 2.419 equazione di Ellipse in termini di p, perpendicolare da F sul thetangent a P, e r, il vettore di raggio FP: 1 = f Lp^ r a i == retto semiclatus. 2.420 Iperbole (Fig. S). 2.421 o, Centro; F, F, Foci.equazione di iperbole, origine a o, ^ y- a2 62 ^ X = OM, y = MP, a = OA= OA. 2.423 equazioni parametriche di hperbola, X = a sec <f), y = b tan 0. </) = angolo XOP, dove P è il punto in cui l'ordinata a T incontra
Figura di Lissajous, artwork Foto Stock
RFD1P2TW–Figura di Lissajous, artwork
. Calcolo differenziale e integrale, un corso introduttivo per le scuole superiori e di ingegneria. Termethe evolute. Se nelle equazioni IV esprimiamo x, y, y, yin termini di x da solo, o di y da solo, o di qualsiasi altra singola variabile, come si può fare generalmente mediante l'equazione del giovenco, avremo le equazioni parametriche dell'evoluto. Nell'esempio 1 del precedente articolo si hanno le parametrequazioni dell'evoluzione della parabola, essendo il parametro x ory, mentre nell'esempio 2 si hanno le equazioni parametriche della teevoluta dell'astroide, essendo il parametro Foto Stock
RM2CEJJ7M–. Calcolo differenziale e integrale, un corso introduttivo per le scuole superiori e di ingegneria. Termethe evolute. Se nelle equazioni IV esprimiamo x, y, y, yin termini di x da solo, o di y da solo, o di qualsiasi altra singola variabile, come si può fare generalmente mediante l'equazione del giovenco, avremo le equazioni parametriche dell'evoluto. Nell'esempio 1 del precedente articolo si hanno le parametrequazioni dell'evoluzione della parabola, essendo il parametro x ory, mentre nell'esempio 2 si hanno le equazioni parametriche della teevoluta dell'astroide, essendo il parametro
Figura di Lissajous, artwork Foto Stock
RFD1P2WP–Figura di Lissajous, artwork
. Calcolo differenziale e integrale, un corso introduttivo per scuole universitarie e di ingegneria. L'equazione del sistema delle normali a qualsiasi curva è / ss x - xi + (y - yx)yx = 0,dove xx può essere considerato come parametro. Differenziare questa equazione a Xu ricordando che sia yx che yx sono funzioni di Xi. Queste due equazioni, / = 0 e -- = 0 per x e y, e quindi ottenere OXx le equazioni parametriche dell'inviluppo delle normali, che si troveranno identiche alle equazioni IV dell'art. 109. 272. Caustiche. Quando i raggi di luce, emananti da un punto fisso, cadono su un concavo Foto Stock
RM2CEJ30A–. Calcolo differenziale e integrale, un corso introduttivo per scuole universitarie e di ingegneria. L'equazione del sistema delle normali a qualsiasi curva è / ss x - xi + (y - yx)yx = 0,dove xx può essere considerato come parametro. Differenziare questa equazione a Xu ricordando che sia yx che yx sono funzioni di Xi. Queste due equazioni, / = 0 e -- = 0 per x e y, e quindi ottenere OXx le equazioni parametriche dell'inviluppo delle normali, che si troveranno identiche alle equazioni IV dell'art. 109. 272. Caustiche. Quando i raggi di luce, emananti da un punto fisso, cadono su un concavo
Figura di Lissajous, artwork Foto Stock
RFD1P2WK–Figura di Lissajous, artwork
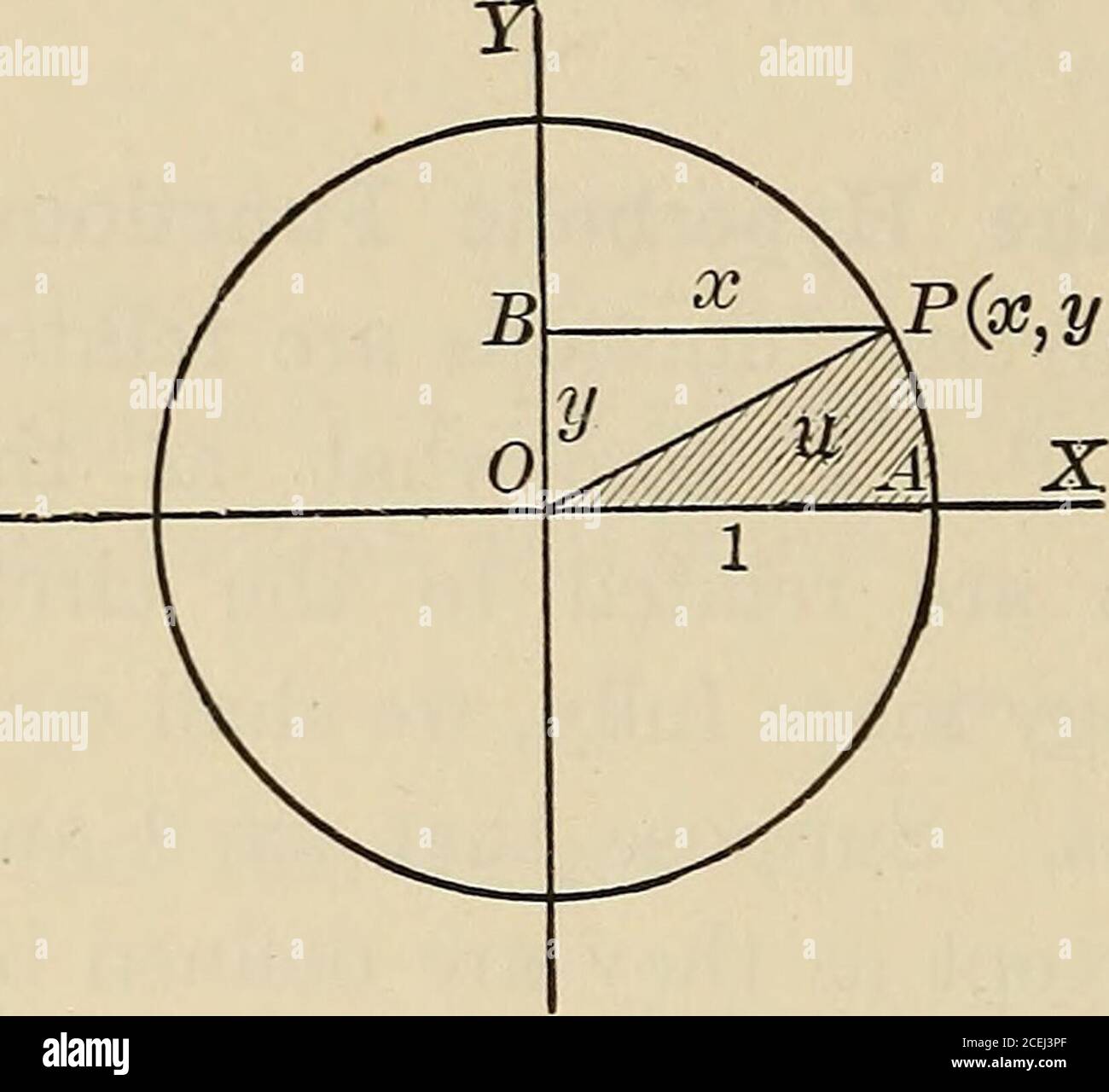. Calcolo differenziale e integrale, un corso introduttivo per collegi e scuole di ingegneria. Er, essere derivato dalla serie di potenza, e da questa relazione edall'equazione del cerchio, x2 + y2 = a2, si potrebbe derivare sottoispezione le equazioni x = a cos 8, y = a sin 6, che sono equazioni parametriche del cerchio. Resta da verificare il significato geometrico del parametro 6. Ora in questo modo possiamo collegare le funzioni iperboliche con l'iperbola equilatera. Dato il relationch2 0 - sh2 0=1, e l'equazione della curva, x2 - y2 = a2, wecan scrivono in onc Foto Stock
RM2CEJ3PF–. Calcolo differenziale e integrale, un corso introduttivo per collegi e scuole di ingegneria. Er, essere derivato dalla serie di potenza, e da questa relazione edall'equazione del cerchio, x2 + y2 = a2, si potrebbe derivare sottoispezione le equazioni x = a cos 8, y = a sin 6, che sono equazioni parametriche del cerchio. Resta da verificare il significato geometrico del parametro 6. Ora in questo modo possiamo collegare le funzioni iperboliche con l'iperbola equilatera. Dato il relationch2 0 - sh2 0=1, e l'equazione della curva, x2 - y2 = a2, wecan scrivono in onc
Figura di Lissajous, artwork Foto Stock
RFD1P2W5–Figura di Lissajous, artwork
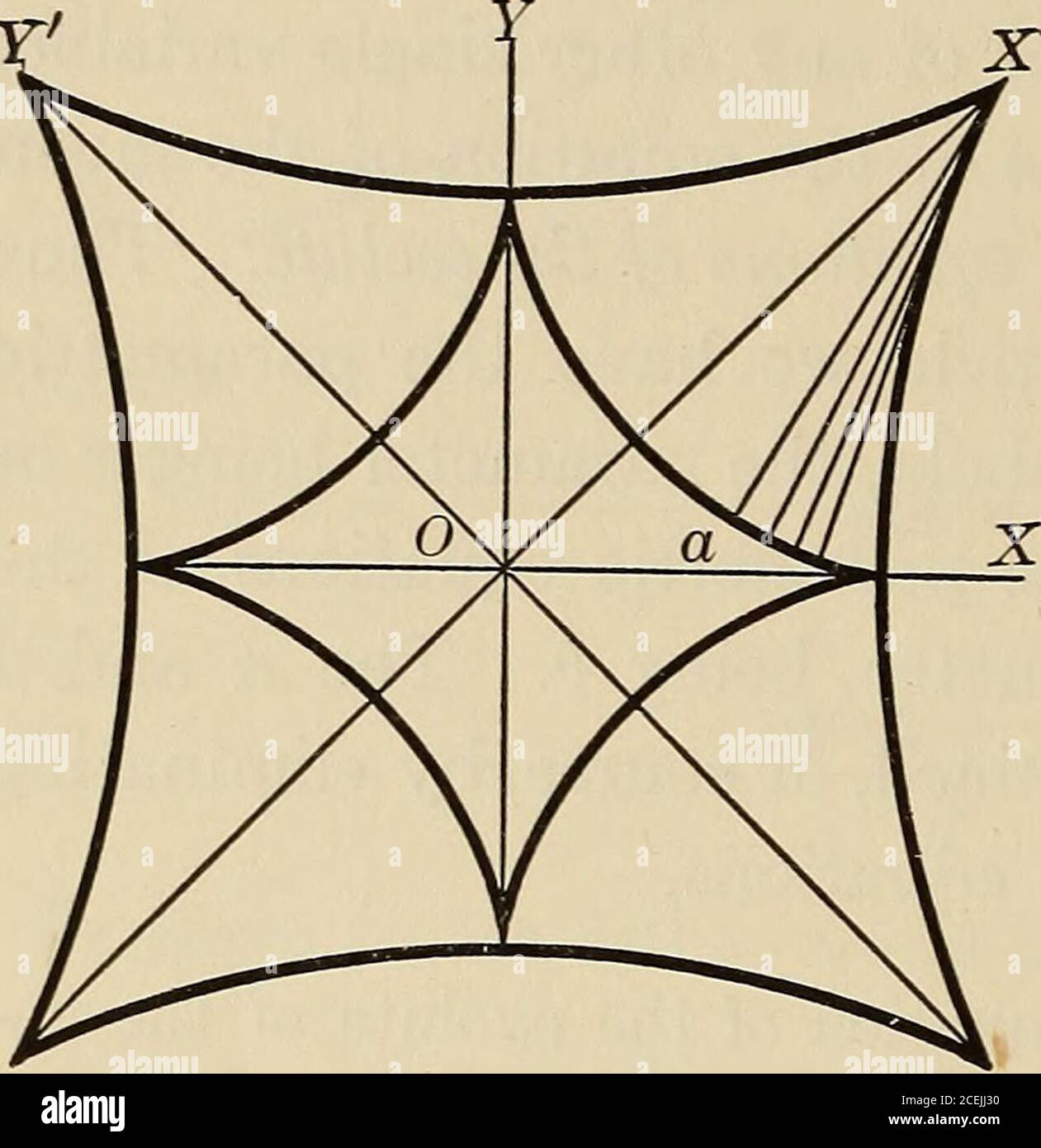. Calcolo differenziale e integrale, un corso introduttivo per scuole superiori e di ingegneria. la, e viceversa. Esempio 2. L'evoluzione dell'astroide. Nell'esempio 2 dell'articolo precedente abbiamo le equazioni parametriche 158 CALCOLO DIFFERENZIALE §111 dell'evoluto dell'astroide nella forma (scrittura x e y al posto di aand 0) x = a cos 0 (1 + 2 sin2 0), y = a sin 0 (1 + 2 cos2 0). Un'idea migliore della forma della curva può essere data dalla sua x e y / equazione, che è ottenuta elimando 0 dalle precedenti equazioni. Questa eliminazione può essere eseguita come segue:x + y = a (cos Foto Stock
RM2CEJJ30–. Calcolo differenziale e integrale, un corso introduttivo per scuole superiori e di ingegneria. la, e viceversa. Esempio 2. L'evoluzione dell'astroide. Nell'esempio 2 dell'articolo precedente abbiamo le equazioni parametriche 158 CALCOLO DIFFERENZIALE §111 dell'evoluto dell'astroide nella forma (scrittura x e y al posto di aand 0) x = a cos 0 (1 + 2 sin2 0), y = a sin 0 (1 + 2 cos2 0). Un'idea migliore della forma della curva può essere data dalla sua x e y / equazione, che è ottenuta elimando 0 dalle precedenti equazioni. Questa eliminazione può essere eseguita come segue:x + y = a (cos
Figura di Lissajous, artwork Foto Stock
RFD1P2WC–Figura di Lissajous, artwork
. Calcolo differenziale e integrale, un corso introduttivo per scuole superiori e di ingegneria. YQ = r cos /3 J»o.l/o»*c / Kt A r x-x X / mr, z - ZQ = r cos 7 = nr, 282 GEOMETRIA DI TRE DIMENSIONI §190 dove (III) x = x0 + IR, y = yoJr mr, z = Zq-- nr. Ora se r è variabile, così sono anche x, y, e z, e come r varia da - oo a +oo, il punto (x, y, z) traccia la linea. Le equazioni (III) sono denominate equazioni parametriche della linea, r essendo il parametro variabileed. 190. Equazione normale del piano. Sia p la lunghezza e a, (3, y gli angoli di direzione della perpendicolare (la normale), Foto Stock
RM2CEJBD8–. Calcolo differenziale e integrale, un corso introduttivo per scuole superiori e di ingegneria. YQ = r cos /3 J»o.l/o»*c / Kt A r x-x X / mr, z - ZQ = r cos 7 = nr, 282 GEOMETRIA DI TRE DIMENSIONI §190 dove (III) x = x0 + IR, y = yoJr mr, z = Zq-- nr. Ora se r è variabile, così sono anche x, y, e z, e come r varia da - oo a +oo, il punto (x, y, z) traccia la linea. Le equazioni (III) sono denominate equazioni parametriche della linea, r essendo il parametro variabileed. 190. Equazione normale del piano. Sia p la lunghezza e a, (3, y gli angoli di direzione della perpendicolare (la normale),
Figura di Lissajous, artwork Foto Stock
RFD1P2WH–Figura di Lissajous, artwork
. Calcolo differenziale e integrale, un corso introduttivo per scuole superiori e di ingegneria. 27. L'evoluta del Lemniscato.2 a cos3 0 25- *=(rnr ^=te> o x = a (1 + cos 0) sin 0,?/ = a sin2 0. 3 VCOs 2 0 2 a sin3 02/ = -- • 3 a/cos 2 0 28. z=^(l-cos0), 547/ = -- (1 - cos 0) sin 0.4a 26. 3 = 4ai2 te, 1-M4or x = 2 a sin 2 0, ?/ = 2 a sin 0 a/2 sin 2 0. 29. x = un peccato 6, y= b cos3 0. 92. Derivazione delle equazioni parametriche. Nell'art. 90 abbiamo abusato di equazioni parametriche razionali del folio di Descartesby sostituendo y = tx nell'equazione x- e ^/-della curva. Itis non sempre poss Foto Stock
RM2CEJT9C–. Calcolo differenziale e integrale, un corso introduttivo per scuole superiori e di ingegneria. 27. L'evoluta del Lemniscato.2 a cos3 0 25- *=(rnr ^=te> o x = a (1 + cos 0) sin 0,?/ = a sin2 0. 3 VCOs 2 0 2 a sin3 02/ = -- • 3 a/cos 2 0 28. z=^(l-cos0), 547/ = -- (1 - cos 0) sin 0.4a 26. 3 = 4ai2 te, 1-M4or x = 2 a sin 2 0, ?/ = 2 a sin 0 a/2 sin 2 0. 29. x = un peccato 6, y= b cos3 0. 92. Derivazione delle equazioni parametriche. Nell'art. 90 abbiamo abusato di equazioni parametriche razionali del folio di Descartesby sostituendo y = tx nell'equazione x- e ^/-della curva. Itis non sempre poss
Figura di Lissajous, artwork Foto Stock
RFD1P2WW–Figura di Lissajous, artwork
Figura di Lissajous, artwork Foto Stock
RFD1P2W3–Figura di Lissajous, artwork
Figura di Lissajous, artwork Foto Stock
RFD1P2WD–Figura di Lissajous, artwork

Risultati della ricerca per Equazione parametrica Foto Stock e Immagini (17)