Geometria non euclidea Immagini Stock
(24)Filtri rapidi:
Geometria non euclidea Immagini Stock
Janos Bolyai (1802-1860) era un matematico ungherese, noto per il suo lavoro in non-geometria euclidea. Dall'età di tredici anni aveva imparato il tartaro e altre forme di meccanica analitica, ricevere istruzioni da suo padre. Egli divenne così ossessionati con Euc Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-janos-bolyai-1802-1860-era-un-matematico-ungherese-noto-per-il-suo-lavoro-in-non-geometria-euclidea-dall-eta-di-tredici-anni-aveva-imparato-il-tartaro-e-altre-forme-di-meccanica-analitica-ricevere-istruzioni-da-suo-padre-egli-divenne-cosi-ossessionati-con-euc-104001492.htmlRMG15JY0–Janos Bolyai (1802-1860) era un matematico ungherese, noto per il suo lavoro in non-geometria euclidea. Dall'età di tredici anni aveva imparato il tartaro e altre forme di meccanica analitica, ricevere istruzioni da suo padre. Egli divenne così ossessionati con Euc
Timbro stampato in Romania mostra un ritratto di un matematico ungherese, fondatore di una geometria non euclidea, Janos Bolyai Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-timbro-stampato-in-romania-mostra-un-ritratto-di-un-matematico-ungherese-fondatore-di-una-geometria-non-euclidea-janos-bolyai-74135444.htmlRME8H4EC–Timbro stampato in Romania mostra un ritratto di un matematico ungherese, fondatore di una geometria non euclidea, Janos Bolyai
Palma de Mallorca fotografata con un obiettivo fisheye, il porto turistico in primo piano Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/palma-de-mallorca-fotografata-con-un-obiettivo-fisheye-il-porto-turistico-in-primo-piano-image430441792.htmlRF2G088W4–Palma de Mallorca fotografata con un obiettivo fisheye, il porto turistico in primo piano
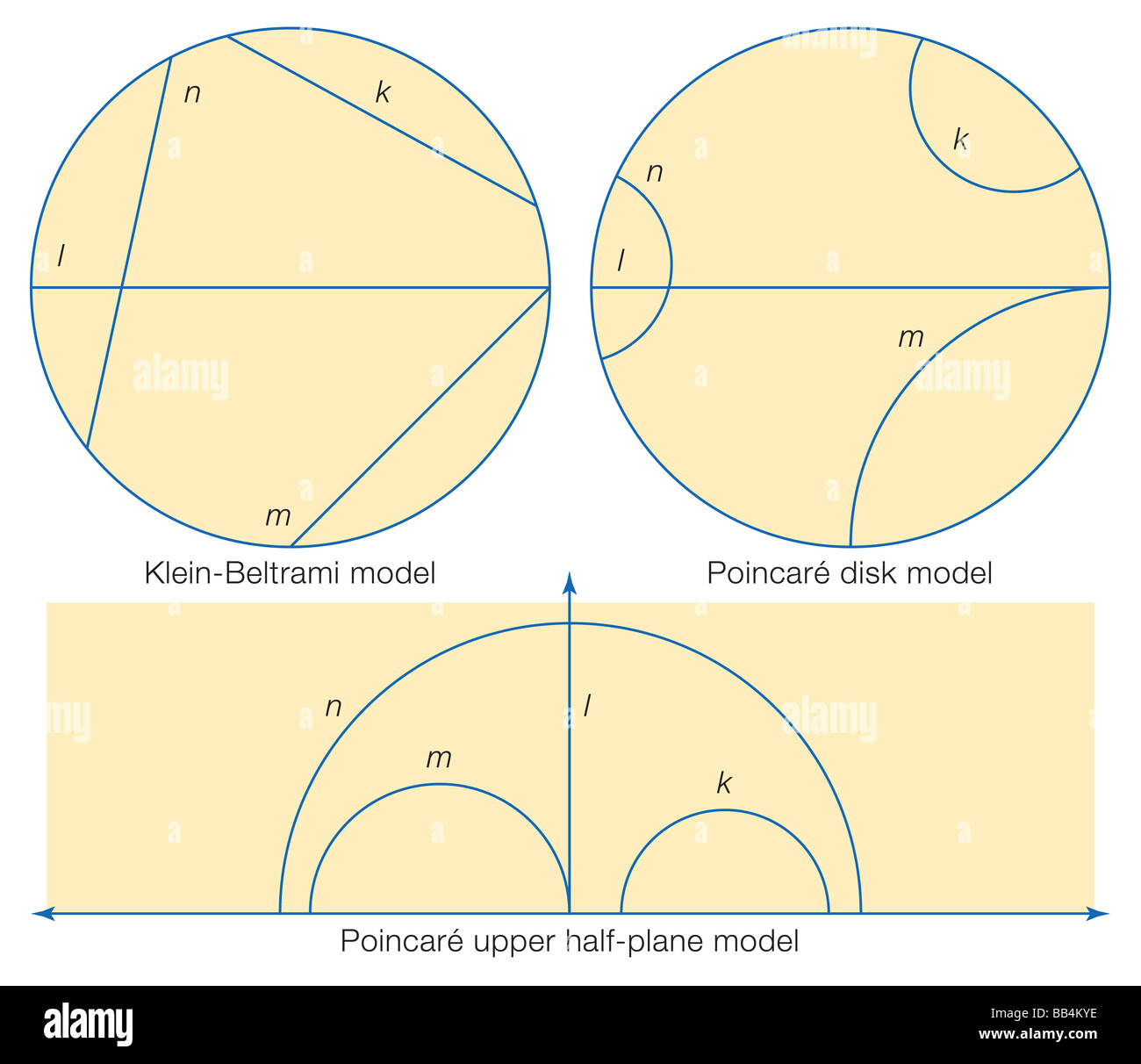Tre modelli di geometria iperbolica: il modello Klein-Beltrami, il disco di Poincaré il modello e la Poincare metà superiore del modello di piano. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-tre-modelli-di-geometria-iperbolica-il-modello-klein-beltrami-il-disco-di-poincare-il-modello-e-la-poincare-meta-superiore-del-modello-di-piano-24075058.htmlRMBB4KYE–Tre modelli di geometria iperbolica: il modello Klein-Beltrami, il disco di Poincaré il modello e la Poincare metà superiore del modello di piano.
LA piazzetta di Oriomoso , immagine circola tagliata con fisheye Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/la-piazzetta-di-oriomoso-immagine-circola-tagliata-con-fisheye-image430980040.htmlRF2G14RC8–LA piazzetta di Oriomoso , immagine circola tagliata con fisheye
Icona Del Concetto Di Geometria Del Vettore 3d Modello Lobachevsky - Immagine Hypertorus Non Euclidea Geometrica Infinita Illustrazione Vettorialehttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/icona-del-concetto-di-geometria-del-vettore-3d-modello-lobachevsky-immagine-hypertorus-non-euclidea-geometrica-infinita-image341980917.htmlRF2ATAG45–Icona Del Concetto Di Geometria Del Vettore 3d Modello Lobachevsky - Immagine Hypertorus Non Euclidea Geometrica Infinita
Cancellata fotografata con un fisheye e tagliata a forma ovale Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancellata-fotografata-con-un-fisheye-e-tagliata-a-forma-ovale-image430441798.htmlRF2G088WA–Cancellata fotografata con un fisheye e tagliata a forma ovale
Vettore Black Hole, Wormhole Concept background - spazio gravitazionale Funnel Trap, geometria Gyperbolic, curvatura negativa ecc Illustrazione Vettorialehttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/vettore-black-hole-wormhole-concept-background-spazio-gravitazionale-funnel-trap-geometria-gyperbolic-curvatura-negativa-ecc-image341947450.htmlRF2AT91CX–Vettore Black Hole, Wormhole Concept background - spazio gravitazionale Funnel Trap, geometria Gyperbolic, curvatura negativa ecc
Kazan, Russia - 15 giugno 2023: Piazza dei Giardini Lobachevsky. Monumento a Lobachevsky, eccellente matematico, fondatore della geometria non euclidea, rettore Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/kazan-russia-15-giugno-2023-piazza-dei-giardini-lobachevsky-monumento-a-lobachevsky-eccellente-matematico-fondatore-della-geometria-non-euclidea-rettore-image568312838.htmlRF2T0GTR2–Kazan, Russia - 15 giugno 2023: Piazza dei Giardini Lobachevsky. Monumento a Lobachevsky, eccellente matematico, fondatore della geometria non euclidea, rettore
Icona Del Concetto Geometrico Non Euclideo Del Modello Vettoriale 3d - Immagine Toroidale Senza Fine Con Bassa Poli Illustrazione Vettorialehttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/icona-del-concetto-geometrico-non-euclideo-del-modello-vettoriale-3d-immagine-toroidale-senza-fine-con-bassa-poli-image341981049.htmlRF2ATAG8W–Icona Del Concetto Geometrico Non Euclideo Del Modello Vettoriale 3d - Immagine Toroidale Senza Fine Con Bassa Poli
GEOMETRIE NON EUCLIDEE Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/geometrie-non-euclidee-image508193064.htmlRM2MEP5C8–GEOMETRIE NON EUCLIDEE
La corte aperta . ng la grande tradizione che è stata interrotta dal romanticMovement del XIX secolo. Bologna, ottobre 1st., 1911. Fedengo Enriques. Contenuti Parziali I Tentativi Di Dimostrare La Postulazione Parallela Dei Precursori Della Geometria Non Euclidea I Fondatori Della Geometria Non Euclidea Il Successivo Sviluppo Della Geometria Non Euclidea I Principi Fondamentali Della Statistica E Degli Euclidi Popolano I Parallels E La Superficie Di Cliffords. Disegno di Clifford-Kleins ProbemIl conilrudion Parallelo non euclideo e altri con alleati- ^rudlionsLa Indipendenza della geometria Projedlive da Eucli Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/la-corte-aperta-ng-la-grande-tradizione-che-e-stata-interrotta-dal-romanticmovement-del-xix-secolo-bologna-ottobre-1st-1911-fedengo-enriques-contenuti-parziali-i-tentativi-di-dimostrare-la-postulazione-parallela-dei-precursori-della-geometria-non-euclidea-i-fondatori-della-geometria-non-euclidea-il-successivo-sviluppo-della-geometria-non-euclidea-i-principi-fondamentali-della-statistica-e-degli-euclidi-popolano-i-parallels-e-la-superficie-di-cliffords-disegno-di-clifford-kleins-probemil-conilrudion-parallelo-non-euclideo-e-altri-con-alleati-rudlionsla-indipendenza-della-geometria-projedlive-da-eucli-image342727647.htmlRM2AWGGH3–La corte aperta . ng la grande tradizione che è stata interrotta dal romanticMovement del XIX secolo. Bologna, ottobre 1st., 1911. Fedengo Enriques. Contenuti Parziali I Tentativi Di Dimostrare La Postulazione Parallela Dei Precursori Della Geometria Non Euclidea I Fondatori Della Geometria Non Euclidea Il Successivo Sviluppo Della Geometria Non Euclidea I Principi Fondamentali Della Statistica E Degli Euclidi Popolano I Parallels E La Superficie Di Cliffords. Disegno di Clifford-Kleins ProbemIl conilrudion Parallelo non euclideo e altri con alleati- ^rudlionsLa Indipendenza della geometria Projedlive da Eucli
La Romania, Targu Mures, Farkas Bolyai, Janos Bolyai, ungherese, matematici, statua, Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-la-romania-targu-mures-farkas-bolyai-janos-bolyai-ungherese-matematici-statua-51095412.htmlRMCY3GM4–La Romania, Targu Mures, Farkas Bolyai, Janos Bolyai, ungherese, matematici, statua,
Spazio di curvatura vettoriale, concetto di Wormhole sfondo - Catenoide, imbuto a foro nero, geometria Gyperbolic, curvatura negativa ecc Illustrazione Vettorialehttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/spazio-di-curvatura-vettoriale-concetto-di-wormhole-sfondo-catenoide-imbuto-a-foro-nero-geometria-gyperbolic-curvatura-negativa-ecc-image341947460.htmlRF2AT91D8–Spazio di curvatura vettoriale, concetto di Wormhole sfondo - Catenoide, imbuto a foro nero, geometria Gyperbolic, curvatura negativa ecc
Matita e libro matematica su alcuni tipi di geometria Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-matita-e-libro-matematica-su-alcuni-tipi-di-geometria-75730175.htmlRFEB5PH3–Matita e libro matematica su alcuni tipi di geometria
Janos Bolyai (1802-1860) era un matematico ungherese, noto per il suo lavoro in non-geometria euclidea. Dall'età di tredici anni aveva imparato il tartaro e altre forme di meccanica analitica, ricevere istruzioni da suo padre. Egli divenne così ossessionati con Euc Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-janos-bolyai-1802-1860-era-un-matematico-ungherese-noto-per-il-suo-lavoro-in-non-geometria-euclidea-dall-eta-di-tredici-anni-aveva-imparato-il-tartaro-e-altre-forme-di-meccanica-analitica-ricevere-istruzioni-da-suo-padre-egli-divenne-cosi-ossessionati-con-euc-104001490.htmlRMG15JXX–Janos Bolyai (1802-1860) era un matematico ungherese, noto per il suo lavoro in non-geometria euclidea. Dall'età di tredici anni aveva imparato il tartaro e altre forme di meccanica analitica, ricevere istruzioni da suo padre. Egli divenne così ossessionati con Euc
Quadrilatero di Omar Khayyam, costruito in uno sforzo per dimostrare la Euclid è postulato concernente le linee parallele superflue. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-quadrilatero-di-omar-khayyam-costruito-in-uno-sforzo-per-dimostrare-la-euclid-e-postulato-concernente-le-linee-parallele-superflue-24074522.htmlRMBB4K8A–Quadrilatero di Omar Khayyam, costruito in uno sforzo per dimostrare la Euclid è postulato concernente le linee parallele superflue.
Cancellata fotografata con un fisheye e tagliata a forma ovale Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancellata-fotografata-con-un-fisheye-e-tagliata-a-forma-ovale-image430441795.htmlRF2G088W7–Cancellata fotografata con un fisheye e tagliata a forma ovale
Kazan, Russia - 15 giugno 2023: Monumento a Lobachevsky, 1896, scultore M.Dillon. Eccezionale matematico, fondatore della geometria non euclidea, rettore Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/kazan-russia-15-giugno-2023-monumento-a-lobachevsky-1896-scultore-m-dillon-eccezionale-matematico-fondatore-della-geometria-non-euclidea-rettore-image567968404.htmlRF2T015DT–Kazan, Russia - 15 giugno 2023: Monumento a Lobachevsky, 1896, scultore M.Dillon. Eccezionale matematico, fondatore della geometria non euclidea, rettore
. L'anatomia della scienza. La scienza. Spazio e geometria 49 a destra si trova la bussola, che nella sua forma più semplice è un pezzo di corda che viene mantenuto teso mentre una estremità è fissata. Il primo strumento si può utilizzare in tutte le nostre geometrie piane, ma il secondo deve essere modificato in conformità con le regole di trans-. 4 FlGURE Non-Euclidean Compass formazione che decidiamo di utilizzare in luogo di rotazione Euclidea. Lasciate che vi mostri ora uno strumento che mi può chiamare un non-euclidean bussola (Figura 4). Esso è costituito da due aste AB e BC, la prima delle quali è fissa e la seconda è consentito di spostarsi su una h Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/l-anatomia-della-scienza-la-scienza-spazio-e-geometria-49-a-destra-si-trova-la-bussola-che-nella-sua-forma-piu-semplice-e-un-pezzo-di-corda-che-viene-mantenuto-teso-mentre-una-estremita-e-fissata-il-primo-strumento-si-puo-utilizzare-in-tutte-le-nostre-geometrie-piane-ma-il-secondo-deve-essere-modificato-in-conformita-con-le-regole-di-trans-4-flgure-non-euclidean-compass-formazione-che-decidiamo-di-utilizzare-in-luogo-di-rotazione-euclidea-lasciate-che-vi-mostri-ora-uno-strumento-che-mi-puo-chiamare-un-non-euclidean-bussola-figura-4-esso-e-costituito-da-due-aste-ab-e-bc-la-prima-delle-quali-e-fissa-e-la-seconda-e-consentito-di-spostarsi-su-una-h-image236813570.htmlRMRN7P3E–. L'anatomia della scienza. La scienza. Spazio e geometria 49 a destra si trova la bussola, che nella sua forma più semplice è un pezzo di corda che viene mantenuto teso mentre una estremità è fissata. Il primo strumento si può utilizzare in tutte le nostre geometrie piane, ma il secondo deve essere modificato in conformità con le regole di trans-. 4 FlGURE Non-Euclidean Compass formazione che decidiamo di utilizzare in luogo di rotazione Euclidea. Lasciate che vi mostri ora uno strumento che mi può chiamare un non-euclidean bussola (Figura 4). Esso è costituito da due aste AB e BC, la prima delle quali è fissa e la seconda è consentito di spostarsi su una h
Curvatura Space-Time Concept Design - sfondo futuristico Hi-Tech Illustrazione Vettorialehttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/curvatura-space-time-concept-design-sfondo-futuristico-hi-tech-image341954880.htmlRF2AT9AX8–Curvatura Space-Time Concept Design - sfondo futuristico Hi-Tech
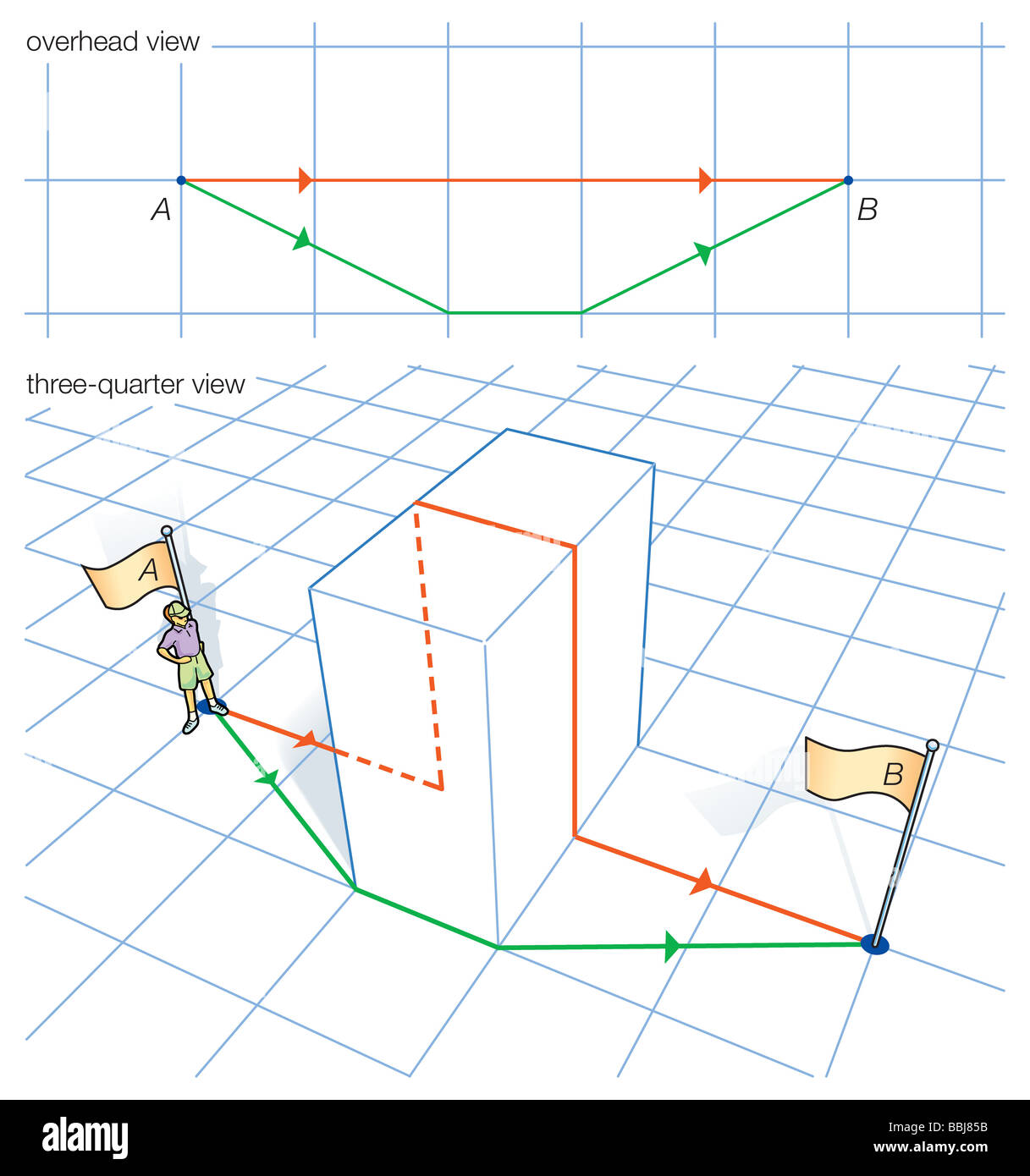La dimostrazione che intrinsecamente una linea diritta (la linea rossa) non è necessariamente la distanza più breve tra due punti. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-la-dimostrazione-che-intrinsecamente-una-linea-diritta-la-linea-rossa-non-e-necessariamente-la-distanza-piu-breve-tra-due-punti-24373143.htmlRMBBJ85B–La dimostrazione che intrinsecamente una linea diritta (la linea rossa) non è necessariamente la distanza più breve tra due punti.
Le funzioni iperboliche cosh x e sinh x. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-le-funzioni-iperboliche-cosh-x-e-sinh-x-24899320.htmlRMBCE79C–Le funzioni iperboliche cosh x e sinh x.
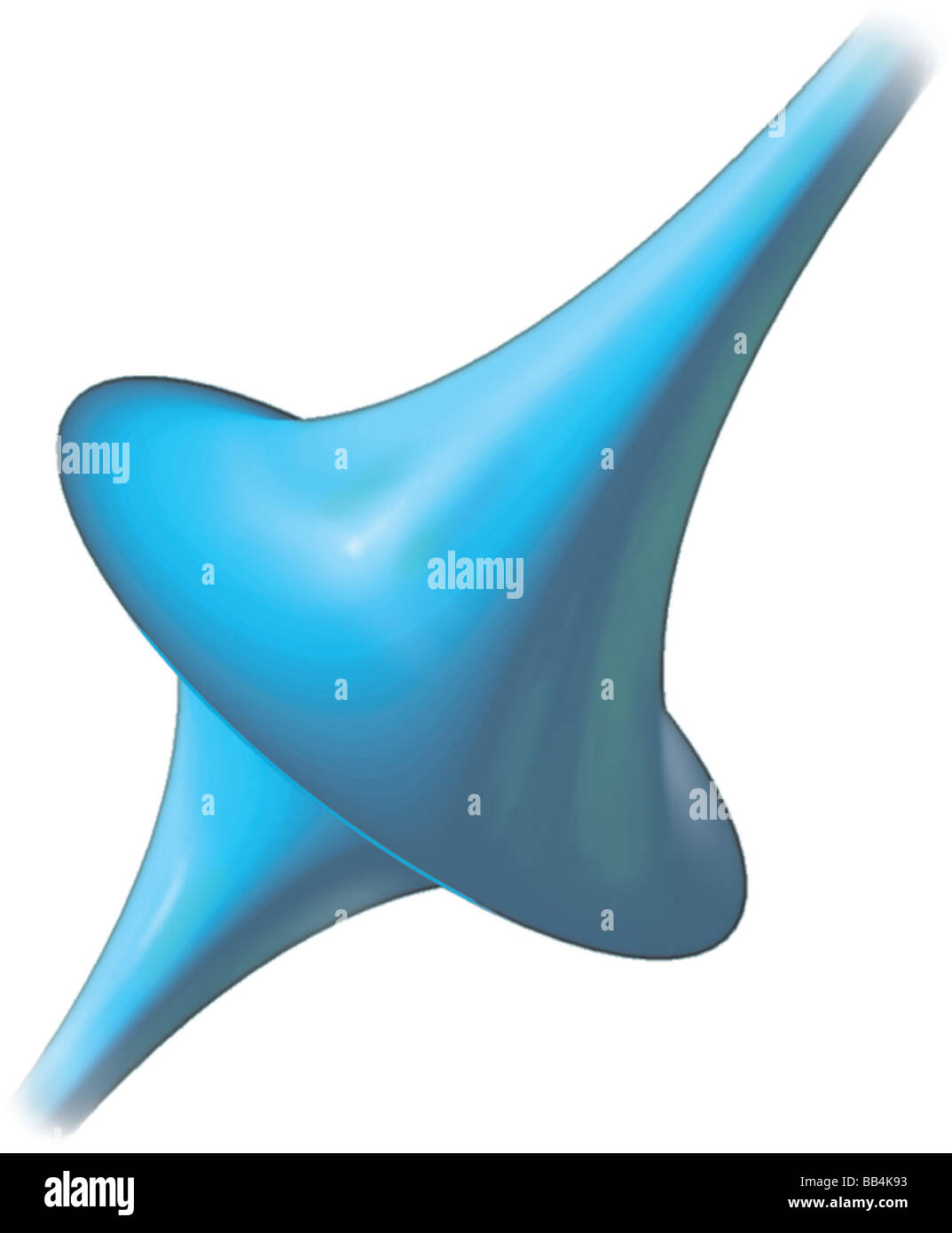La pseudosphere ha curvatura costante negativa; si rastrema all'infinito in entrambe le direzioni in allontanamento dal disco centrale. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-la-pseudosphere-ha-curvatura-costante-negativa-si-rastrema-all-infinito-in-entrambe-le-direzioni-in-allontanamento-dal-disco-centrale-24074543.htmlRMBB4K93–La pseudosphere ha curvatura costante negativa; si rastrema all'infinito in entrambe le direzioni in allontanamento dal disco centrale.
