Geometria proiettiva Immagini Stock
(524)Filtri rapidi:
Geometria proiettiva Immagini Stock
 Jean Victor Poncelet. 1788-1867. Ingegnere matematico francese Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/jean-victor-poncelet-1788-1867-ingegnere-matematico-francese-image572169795.html
Jean Victor Poncelet. 1788-1867. Ingegnere matematico francese Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/jean-victor-poncelet-1788-1867-ingegnere-matematico-francese-image572169795.htmlRM2T6TGBF–Jean Victor Poncelet. 1788-1867. Ingegnere matematico francese
 Jean Victor Poncelet Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-jean-victor-poncelet-50319382.html
Jean Victor Poncelet Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-jean-victor-poncelet-50319382.htmlRFCWT6TP–Jean Victor Poncelet
 Jean Victor Poncelet 1788-1867. Ingegnere matematico francese Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/jean-victor-poncelet-1788-1867-ingegnere-matematico-francese-image572169851.html
Jean Victor Poncelet 1788-1867. Ingegnere matematico francese Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/jean-victor-poncelet-1788-1867-ingegnere-matematico-francese-image572169851.htmlRM2T6TGDF–Jean Victor Poncelet 1788-1867. Ingegnere matematico francese
 Incisione antica di un ritratto di Blaise Pascal, matematico francese, fisico e filosofo religioso. Ha contribuito a creare due nuove aree principali di Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/incisione-antica-di-un-ritratto-di-blaise-pascal-matematico-francese-fisico-e-filosofo-religioso-ha-contribuito-a-creare-due-nuove-aree-principali-di-image414187907.html
Incisione antica di un ritratto di Blaise Pascal, matematico francese, fisico e filosofo religioso. Ha contribuito a creare due nuove aree principali di Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/incisione-antica-di-un-ritratto-di-blaise-pascal-matematico-francese-fisico-e-filosofo-religioso-ha-contribuito-a-creare-due-nuove-aree-principali-di-image414187907.htmlRF2F1RTW7–Incisione antica di un ritratto di Blaise Pascal, matematico francese, fisico e filosofo religioso. Ha contribuito a creare due nuove aree principali di
![Girard Desargues (Parigi, 21 febbraio 1591 – Parigi, settembre 1661) è stato un matematico e ingegnere francese, considerato uno dei fondatori della geometria proiettiva. Dal libro la ciencia y sus hombres : vidas de los sabios ilustres desde la antigüedad hasta el siglo XIX T. 2 [Scienza e suoi uomini: Vite dei saggi illustri dall'antichità al XIX secolo Vol 2] di Figuier, Luigi, (1819-1894); Casabó y Pagés, Pelegrín, n. 1831 pubblicato a Barcellona da D. Jaime Seix, editore , 1879 (Imprenta de Baseda y Giró) Foto Stock Girard Desargues (Parigi, 21 febbraio 1591 – Parigi, settembre 1661) è stato un matematico e ingegnere francese, considerato uno dei fondatori della geometria proiettiva. Dal libro la ciencia y sus hombres : vidas de los sabios ilustres desde la antigüedad hasta el siglo XIX T. 2 [Scienza e suoi uomini: Vite dei saggi illustri dall'antichità al XIX secolo Vol 2] di Figuier, Luigi, (1819-1894); Casabó y Pagés, Pelegrín, n. 1831 pubblicato a Barcellona da D. Jaime Seix, editore , 1879 (Imprenta de Baseda y Giró) Foto Stock](https://c8.alamy.com/compit/2catr7y/girard-desargues-parigi-21-febbraio-1591-parigi-settembre-1661-e-stato-un-matematico-e-ingegnere-francese-considerato-uno-dei-fondatori-della-geometria-proiettiva-dal-libro-la-ciencia-y-sus-hombres-vidas-de-los-sabios-ilustres-desde-la-antiguedad-hasta-el-siglo-xix-t-2-scienza-e-suoi-uomini-vite-dei-saggi-illustri-dall-antichita-al-xix-secolo-vol-2-di-figuier-luigi-1819-1894-casabo-y-pages-pelegrin-n-1831-pubblicato-a-barcellona-da-d-jaime-seix-editore-1879-imprenta-de-baseda-y-giro-2catr7y.jpg) Girard Desargues (Parigi, 21 febbraio 1591 – Parigi, settembre 1661) è stato un matematico e ingegnere francese, considerato uno dei fondatori della geometria proiettiva. Dal libro la ciencia y sus hombres : vidas de los sabios ilustres desde la antigüedad hasta el siglo XIX T. 2 [Scienza e suoi uomini: Vite dei saggi illustri dall'antichità al XIX secolo Vol 2] di Figuier, Luigi, (1819-1894); Casabó y Pagés, Pelegrín, n. 1831 pubblicato a Barcellona da D. Jaime Seix, editore , 1879 (Imprenta de Baseda y Giró) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/girard-desargues-parigi-21-febbraio-1591-parigi-settembre-1661-e-stato-un-matematico-e-ingegnere-francese-considerato-uno-dei-fondatori-della-geometria-proiettiva-dal-libro-la-ciencia-y-sus-hombres-vidas-de-los-sabios-ilustres-desde-la-antiguedad-hasta-el-siglo-xix-t-2-scienza-e-suoi-uomini-vite-dei-saggi-illustri-dall-antichita-al-xix-secolo-vol-2-di-figuier-luigi-1819-1894-casabo-y-pages-pelegrin-n-1831-pubblicato-a-barcellona-da-d-jaime-seix-editore-1879-imprenta-de-baseda-y-giro-image368109391.html
Girard Desargues (Parigi, 21 febbraio 1591 – Parigi, settembre 1661) è stato un matematico e ingegnere francese, considerato uno dei fondatori della geometria proiettiva. Dal libro la ciencia y sus hombres : vidas de los sabios ilustres desde la antigüedad hasta el siglo XIX T. 2 [Scienza e suoi uomini: Vite dei saggi illustri dall'antichità al XIX secolo Vol 2] di Figuier, Luigi, (1819-1894); Casabó y Pagés, Pelegrín, n. 1831 pubblicato a Barcellona da D. Jaime Seix, editore , 1879 (Imprenta de Baseda y Giró) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/girard-desargues-parigi-21-febbraio-1591-parigi-settembre-1661-e-stato-un-matematico-e-ingegnere-francese-considerato-uno-dei-fondatori-della-geometria-proiettiva-dal-libro-la-ciencia-y-sus-hombres-vidas-de-los-sabios-ilustres-desde-la-antiguedad-hasta-el-siglo-xix-t-2-scienza-e-suoi-uomini-vite-dei-saggi-illustri-dall-antichita-al-xix-secolo-vol-2-di-figuier-luigi-1819-1894-casabo-y-pages-pelegrin-n-1831-pubblicato-a-barcellona-da-d-jaime-seix-editore-1879-imprenta-de-baseda-y-giro-image368109391.htmlRM2CATR7Y–Girard Desargues (Parigi, 21 febbraio 1591 – Parigi, settembre 1661) è stato un matematico e ingegnere francese, considerato uno dei fondatori della geometria proiettiva. Dal libro la ciencia y sus hombres : vidas de los sabios ilustres desde la antigüedad hasta el siglo XIX T. 2 [Scienza e suoi uomini: Vite dei saggi illustri dall'antichità al XIX secolo Vol 2] di Figuier, Luigi, (1819-1894); Casabó y Pagés, Pelegrín, n. 1831 pubblicato a Barcellona da D. Jaime Seix, editore , 1879 (Imprenta de Baseda y Giró)
 Vista ravvicinata della geometria di puntamento rivelatori della tigre esperimento presso il laboratorio triumf a Vancouver Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/vista-ravvicinata-della-geometria-di-puntamento-rivelatori-della-tigre-esperimento-presso-il-laboratorio-triumf-a-vancouver-image66744866.html
Vista ravvicinata della geometria di puntamento rivelatori della tigre esperimento presso il laboratorio triumf a Vancouver Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/vista-ravvicinata-della-geometria-di-puntamento-rivelatori-della-tigre-esperimento-presso-il-laboratorio-triumf-a-vancouver-image66744866.htmlRMDTGDN6–Vista ravvicinata della geometria di puntamento rivelatori della tigre esperimento presso il laboratorio triumf a Vancouver
 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184207.html
'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184207.htmlRMGPJ5J7–'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
 Encyclopédie, prospettiva Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/encyclop-die-prospettiva-image352803550.html
Encyclop√©die, prospettiva Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/encyclop-die-prospettiva-image352803550.htmlRM2BDYGEP–Encyclop√©die, prospettiva
 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184283.html
'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184283.htmlRMGPJ5MY–'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
 Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-87033146.html
Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-87033146.htmlRMF1GKJJ–Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915)
 Linee rette a ritmo con l'architettura della facciata di un edificio di uffici. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/linee-rette-a-ritmo-con-l-architettura-della-facciata-di-un-edificio-di-uffici-image516378572.html
Linee rette a ritmo con l'architettura della facciata di un edificio di uffici. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/linee-rette-a-ritmo-con-l-architettura-della-facciata-di-un-edificio-di-uffici-image516378572.htmlRF2N0323T–Linee rette a ritmo con l'architettura della facciata di un edificio di uffici.
 Vuoto passi anfiteatro in pietra bianca. C'è armonia in edifici vuoti. Le curve parallele si prega di occhi e di portare la pace al popolo OCD Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/vuoto-passi-anfiteatro-in-pietra-bianca-c-e-armonia-in-edifici-vuoti-le-curve-parallele-si-prega-di-occhi-e-di-portare-la-pace-al-popolo-ocd-image222522404.html
Vuoto passi anfiteatro in pietra bianca. C'è armonia in edifici vuoti. Le curve parallele si prega di occhi e di portare la pace al popolo OCD Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/vuoto-passi-anfiteatro-in-pietra-bianca-c-e-armonia-in-edifici-vuoti-le-curve-parallele-si-prega-di-occhi-e-di-portare-la-pace-al-popolo-ocd-image222522404.htmlRFPX0NGM–Vuoto passi anfiteatro in pietra bianca. C'è armonia in edifici vuoti. Le curve parallele si prega di occhi e di portare la pace al popolo OCD
 Illustrazione di un continuo e una funzione discontinua. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-illustrazione-di-un-continuo-e-una-funzione-discontinua-24899309.html
Illustrazione di un continuo e una funzione discontinua. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-illustrazione-di-un-continuo-e-una-funzione-discontinua-24899309.htmlRMBCE791–Illustrazione di un continuo e una funzione discontinua.
 Cancun, Messico; Lug 15 2018: metallo ringhiera bianca con alcuni sport arrugginito. punto di fuga di linee rette dirigere lo sguardo Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-metallo-ringhiera-bianca-con-alcuni-sport-arrugginito-punto-di-fuga-di-linee-rette-dirigere-lo-sguardo-image214366334.html
Cancun, Messico; Lug 15 2018: metallo ringhiera bianca con alcuni sport arrugginito. punto di fuga di linee rette dirigere lo sguardo Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-metallo-ringhiera-bianca-con-alcuni-sport-arrugginito-punto-di-fuga-di-linee-rette-dirigere-lo-sguardo-image214366334.htmlRFPCN6CE–Cancun, Messico; Lug 15 2018: metallo ringhiera bianca con alcuni sport arrugginito. punto di fuga di linee rette dirigere lo sguardo
 Austin, Texas USA 17 luglio 2020: Corsie vuote nell'ultima serata di bowling a Dart Bowl, come l'azienda di proprietà locale, aperto per 64 anni, chiude a causa delle lotte economiche e della pandemia COVID-19. Credit: Bob Daemmrich/Alamy Live News Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/austin-texas-usa-17-luglio-2020-corsie-vuote-nell-ultima-serata-di-bowling-a-dart-bowl-come-l-azienda-di-proprieta-locale-aperto-per-64-anni-chiude-a-causa-delle-lotte-economiche-e-della-pandemia-covid-19-credit-bob-daemmrich-alamy-live-news-image366367045.html
Austin, Texas USA 17 luglio 2020: Corsie vuote nell'ultima serata di bowling a Dart Bowl, come l'azienda di proprietà locale, aperto per 64 anni, chiude a causa delle lotte economiche e della pandemia COVID-19. Credit: Bob Daemmrich/Alamy Live News Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/austin-texas-usa-17-luglio-2020-corsie-vuote-nell-ultima-serata-di-bowling-a-dart-bowl-come-l-azienda-di-proprieta-locale-aperto-per-64-anni-chiude-a-causa-delle-lotte-economiche-e-della-pandemia-covid-19-credit-bob-daemmrich-alamy-live-news-image366367045.htmlRM2C81CW9–Austin, Texas USA 17 luglio 2020: Corsie vuote nell'ultima serata di bowling a Dart Bowl, come l'azienda di proprietà locale, aperto per 64 anni, chiude a causa delle lotte economiche e della pandemia COVID-19. Credit: Bob Daemmrich/Alamy Live News
 . I principi della geometria proiettiva applicati alla linea retta e conica . = ()b^C^ = 1. ■. Dalla conversazione di Carnots Theoremthe sei punti sono su un conico.. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/i-principi-della-geometria-proiettiva-applicati-alla-linea-retta-e-conica-b-c-1-dalla-conversazione-di-carnots-theoremthe-sei-punti-sono-su-un-conico-image372352294.html
. I principi della geometria proiettiva applicati alla linea retta e conica . = ()b^C^ = 1. ■. Dalla conversazione di Carnots Theoremthe sei punti sono su un conico.. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/i-principi-della-geometria-proiettiva-applicati-alla-linea-retta-e-conica-b-c-1-dalla-conversazione-di-carnots-theoremthe-sei-punti-sono-su-un-conico-image372352294.htmlRM2CHP346–. I principi della geometria proiettiva applicati alla linea retta e conica . = ()b^C^ = 1. ■. Dalla conversazione di Carnots Theoremthe sei punti sono su un conico..
 Ritratto vettoriale ad acquerello Blaise Pascal con contorni dell'inchiostro. Matematico francese, fisico, inventore, scrittore e teologo cattolico. Illustrazione Vettorialehttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/ritratto-vettoriale-ad-acquerello-blaise-pascal-con-contorni-dell-inchiostro-matematico-francese-fisico-inventore-scrittore-e-teologo-cattolico-image434304699.html
Ritratto vettoriale ad acquerello Blaise Pascal con contorni dell'inchiostro. Matematico francese, fisico, inventore, scrittore e teologo cattolico. Illustrazione Vettorialehttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/ritratto-vettoriale-ad-acquerello-blaise-pascal-con-contorni-dell-inchiostro-matematico-francese-fisico-inventore-scrittore-e-teologo-cattolico-image434304699.htmlRF2G6G823–Ritratto vettoriale ad acquerello Blaise Pascal con contorni dell'inchiostro. Matematico francese, fisico, inventore, scrittore e teologo cattolico.
 Un primo corso di Geometria proiettiva (1913) (14773266561) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-un-primo-corso-di-geometria-proiettiva-1913-14773266561-173096821.html
Un primo corso di Geometria proiettiva (1913) (14773266561) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-un-primo-corso-di-geometria-proiettiva-1913-14773266561-173096821.htmlRMM1H6N9–Un primo corso di Geometria proiettiva (1913) (14773266561)
 Ritratto di Ernest Julius Wilcynski. 1900 Ernest Julius Wilcynski (1876-1932) matematico tedesco-americano che ha contribuito all'astro matematico Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/ritratto-di-ernest-julius-wilcynski-1900-ernest-julius-wilcynski-1876-1932-matematico-tedesco-americano-che-ha-contribuito-all-astro-matematico-image465661491.html
Ritratto di Ernest Julius Wilcynski. 1900 Ernest Julius Wilcynski (1876-1932) matematico tedesco-americano che ha contribuito all'astro matematico Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/ritratto-di-ernest-julius-wilcynski-1900-ernest-julius-wilcynski-1876-1932-matematico-tedesco-americano-che-ha-contribuito-all-astro-matematico-image465661491.htmlRM2J1GKYF–Ritratto di Ernest Julius Wilcynski. 1900 Ernest Julius Wilcynski (1876-1932) matematico tedesco-americano che ha contribuito all'astro matematico
 Illustrazione del teorema di Brianchon isolata sul bianco Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/illustrazione-del-teorema-di-brianchon-isolata-sul-bianco-image602019086.html
Illustrazione del teorema di Brianchon isolata sul bianco Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/illustrazione-del-teorema-di-brianchon-isolata-sul-bianco-image602019086.htmlRF2WYC9DJ–Illustrazione del teorema di Brianchon isolata sul bianco
 Blaise Pascal (Parigi, 19 giugno 1623 – Parigi, 19 agosto 1662) è stato un . Era un prodigio infantile che era istruito da suo padre, un collettore fiscale a Rouen. Il primo lavoro matematico di Pascal era sulle sezioni di conics; scrisse un trattato significativo sul tema della geometria proiettiva all'età di 16 anni. In seguito ha corrisposto con Pierre de Fermat sulla teoria della probabilità, influenzando fortemente lo sviluppo dell'economia moderna e della scienza sociale. Nel 1642, mentre era ancora un adolescente, iniziò un lavoro pionieristico sul calcolo del mac Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/blaise-pascal-parigi-19-giugno-1623-parigi-19-agosto-1662-e-stato-un-era-un-prodigio-infantile-che-era-istruito-da-suo-padre-un-collettore-fiscale-a-rouen-il-primo-lavoro-matematico-di-pascal-era-sulle-sezioni-di-conics-scrisse-un-trattato-significativo-sul-tema-della-geometria-proiettiva-all-eta-di-16-anni-in-seguito-ha-corrisposto-con-pierre-de-fermat-sulla-teoria-della-probabilita-influenzando-fortemente-lo-sviluppo-dell-economia-moderna-e-della-scienza-sociale-nel-1642-mentre-era-ancora-un-adolescente-inizio-un-lavoro-pionieristico-sul-calcolo-del-mac-image386253526.html
Blaise Pascal (Parigi, 19 giugno 1623 – Parigi, 19 agosto 1662) è stato un . Era un prodigio infantile che era istruito da suo padre, un collettore fiscale a Rouen. Il primo lavoro matematico di Pascal era sulle sezioni di conics; scrisse un trattato significativo sul tema della geometria proiettiva all'età di 16 anni. In seguito ha corrisposto con Pierre de Fermat sulla teoria della probabilità, influenzando fortemente lo sviluppo dell'economia moderna e della scienza sociale. Nel 1642, mentre era ancora un adolescente, iniziò un lavoro pionieristico sul calcolo del mac Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/blaise-pascal-parigi-19-giugno-1623-parigi-19-agosto-1662-e-stato-un-era-un-prodigio-infantile-che-era-istruito-da-suo-padre-un-collettore-fiscale-a-rouen-il-primo-lavoro-matematico-di-pascal-era-sulle-sezioni-di-conics-scrisse-un-trattato-significativo-sul-tema-della-geometria-proiettiva-all-eta-di-16-anni-in-seguito-ha-corrisposto-con-pierre-de-fermat-sulla-teoria-della-probabilita-influenzando-fortemente-lo-sviluppo-dell-economia-moderna-e-della-scienza-sociale-nel-1642-mentre-era-ancora-un-adolescente-inizio-un-lavoro-pionieristico-sul-calcolo-del-mac-image386253526.htmlRF2DCBA8P–Blaise Pascal (Parigi, 19 giugno 1623 – Parigi, 19 agosto 1662) è stato un . Era un prodigio infantile che era istruito da suo padre, un collettore fiscale a Rouen. Il primo lavoro matematico di Pascal era sulle sezioni di conics; scrisse un trattato significativo sul tema della geometria proiettiva all'età di 16 anni. In seguito ha corrisposto con Pierre de Fermat sulla teoria della probabilità, influenzando fortemente lo sviluppo dell'economia moderna e della scienza sociale. Nel 1642, mentre era ancora un adolescente, iniziò un lavoro pionieristico sul calcolo del mac
 Vista parziale della tigre esperimento a triumf a Vancouver Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/vista-parziale-della-tigre-esperimento-a-triumf-a-vancouver-image66745177.html
Vista parziale della tigre esperimento a triumf a Vancouver Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/vista-parziale-della-tigre-esperimento-a-triumf-a-vancouver-image66745177.htmlRMDTGE49–Vista parziale della tigre esperimento a triumf a Vancouver
 Uso della prospettiva, 1618 Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/uso-della-prospettiva-1618-image352803558.html
Uso della prospettiva, 1618 Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/uso-della-prospettiva-1618-image352803558.htmlRM2BDYGF2–Uso della prospettiva, 1618
 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184267.html
'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184267.htmlRMGPJ5MB–'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
 Jean-Victor Poncelet, ingegnere francese e matematico Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/jean-victor-poncelet-ingegnere-francese-e-matematico-image352788936.html
Jean-Victor Poncelet, ingegnere francese e matematico Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/jean-victor-poncelet-ingegnere-francese-e-matematico-image352788936.htmlRM2BDXWTT–Jean-Victor Poncelet, ingegnere francese e matematico
 Il ritmo dei condizionatori d'aria sulla facciata del vecchio edificio di uffici contro il cielo blu. Immagine verticale. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/il-ritmo-dei-condizionatori-d-aria-sulla-facciata-del-vecchio-edificio-di-uffici-contro-il-cielo-blu-immagine-verticale-image511625444.html
Il ritmo dei condizionatori d'aria sulla facciata del vecchio edificio di uffici contro il cielo blu. Immagine verticale. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/il-ritmo-dei-condizionatori-d-aria-sulla-facciata-del-vecchio-edificio-di-uffici-contro-il-cielo-blu-immagine-verticale-image511625444.htmlRF2MMAFD8–Il ritmo dei condizionatori d'aria sulla facciata del vecchio edificio di uffici contro il cielo blu. Immagine verticale.
 Una tavola circolare su cui una vista griglia è stato posizionato per la visualizzazione di una città con un fiume. Incisione storica, probabilmente del XVI secolo. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/una-tavola-circolare-su-cui-una-vista-griglia-e-stato-posizionato-per-la-visualizzazione-di-una-citta-con-un-fiume-incisione-storica-probabilmente-del-xvi-secolo-image246624656.html
Una tavola circolare su cui una vista griglia è stato posizionato per la visualizzazione di una città con un fiume. Incisione storica, probabilmente del XVI secolo. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/una-tavola-circolare-su-cui-una-vista-griglia-e-stato-posizionato-per-la-visualizzazione-di-una-citta-con-un-fiume-incisione-storica-probabilmente-del-xvi-secolo-image246624656.htmlRMT96M7C–Una tavola circolare su cui una vista griglia è stato posizionato per la visualizzazione di una città con un fiume. Incisione storica, probabilmente del XVI secolo.
 Versione proiettiva di Euclide del teorema fondamentale di somiglianza. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-versione-proiettiva-di-euclide-del-teorema-fondamentale-di-somiglianza-24373152.html
Versione proiettiva di Euclide del teorema fondamentale di somiglianza. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-versione-proiettiva-di-euclide-del-teorema-fondamentale-di-somiglianza-24373152.htmlRMBBJ85M–Versione proiettiva di Euclide del teorema fondamentale di somiglianza.
 Cancun, Messico; Lug 15 2018: rampa circolare di ingresso. Moderno e minimalista struttura in calcestruzzo. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-rampa-circolare-di-ingresso-moderno-e-minimalista-struttura-in-calcestruzzo-image214366340.html
Cancun, Messico; Lug 15 2018: rampa circolare di ingresso. Moderno e minimalista struttura in calcestruzzo. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-rampa-circolare-di-ingresso-moderno-e-minimalista-struttura-in-calcestruzzo-image214366340.htmlRFPCN6CM–Cancun, Messico; Lug 15 2018: rampa circolare di ingresso. Moderno e minimalista struttura in calcestruzzo.
 Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-96758992.html
Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-96758992.htmlRMFHBN28–Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915)
 . I principi della geometria proiettiva applicati alla linea retta e conica . OL. OST sin LOB = 1. ■.lo OLBL • CL OC&mfiOL^OL.OBOL.OC 23-2 356 principi della geometria proiettiva Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/i-principi-della-geometria-proiettiva-applicati-alla-linea-retta-e-conica-ol-ost-sin-lob-1-lo-olbl-cl-oc-mfiol-ol-obol-oc-23-2-356-principi-della-geometria-proiettiva-image372311407.html
. I principi della geometria proiettiva applicati alla linea retta e conica . OL. OST sin LOB = 1. ■.lo OLBL • CL OC&mfiOL^OL.OBOL.OC 23-2 356 principi della geometria proiettiva Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/i-principi-della-geometria-proiettiva-applicati-alla-linea-retta-e-conica-ol-ost-sin-lob-1-lo-olbl-cl-oc-mfiol-ol-obol-oc-23-2-356-principi-della-geometria-proiettiva-image372311407.htmlRM2CHM6YY–. I principi della geometria proiettiva applicati alla linea retta e conica . OL. OST sin LOB = 1. ■.lo OLBL • CL OC&mfiOL^OL.OBOL.OC 23-2 356 principi della geometria proiettiva
 Blaise Pascal (Parigi, 19 giugno 1623 – Parigi, 19 agosto 1662) è stato un . Era un prodigio infantile che era istruito da suo padre, un collettore fiscale a Rouen. Il primo lavoro matematico di Pascal era sulle sezioni di conics; scrisse un trattato significativo sul tema della geometria proiettiva all'età di 16 anni. In seguito ha corrisposto con Pierre de Fermat sulla teoria della probabilità, influenzando fortemente lo sviluppo dell'economia moderna e della scienza sociale. Nel 1642, mentre era ancora un adolescente, iniziò un lavoro pionieristico sul calcolo del mac Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/blaise-pascal-parigi-19-giugno-1623-parigi-19-agosto-1662-e-stato-un-era-un-prodigio-infantile-che-era-istruito-da-suo-padre-un-collettore-fiscale-a-rouen-il-primo-lavoro-matematico-di-pascal-era-sulle-sezioni-di-conics-scrisse-un-trattato-significativo-sul-tema-della-geometria-proiettiva-all-eta-di-16-anni-in-seguito-ha-corrisposto-con-pierre-de-fermat-sulla-teoria-della-probabilita-influenzando-fortemente-lo-sviluppo-dell-economia-moderna-e-della-scienza-sociale-nel-1642-mentre-era-ancora-un-adolescente-inizio-un-lavoro-pionieristico-sul-calcolo-del-mac-image386253560.html
Blaise Pascal (Parigi, 19 giugno 1623 – Parigi, 19 agosto 1662) è stato un . Era un prodigio infantile che era istruito da suo padre, un collettore fiscale a Rouen. Il primo lavoro matematico di Pascal era sulle sezioni di conics; scrisse un trattato significativo sul tema della geometria proiettiva all'età di 16 anni. In seguito ha corrisposto con Pierre de Fermat sulla teoria della probabilità, influenzando fortemente lo sviluppo dell'economia moderna e della scienza sociale. Nel 1642, mentre era ancora un adolescente, iniziò un lavoro pionieristico sul calcolo del mac Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/blaise-pascal-parigi-19-giugno-1623-parigi-19-agosto-1662-e-stato-un-era-un-prodigio-infantile-che-era-istruito-da-suo-padre-un-collettore-fiscale-a-rouen-il-primo-lavoro-matematico-di-pascal-era-sulle-sezioni-di-conics-scrisse-un-trattato-significativo-sul-tema-della-geometria-proiettiva-all-eta-di-16-anni-in-seguito-ha-corrisposto-con-pierre-de-fermat-sulla-teoria-della-probabilita-influenzando-fortemente-lo-sviluppo-dell-economia-moderna-e-della-scienza-sociale-nel-1642-mentre-era-ancora-un-adolescente-inizio-un-lavoro-pionieristico-sul-calcolo-del-mac-image386253560.htmlRF2DCBAA0–Blaise Pascal (Parigi, 19 giugno 1623 – Parigi, 19 agosto 1662) è stato un . Era un prodigio infantile che era istruito da suo padre, un collettore fiscale a Rouen. Il primo lavoro matematico di Pascal era sulle sezioni di conics; scrisse un trattato significativo sul tema della geometria proiettiva all'età di 16 anni. In seguito ha corrisposto con Pierre de Fermat sulla teoria della probabilità, influenzando fortemente lo sviluppo dell'economia moderna e della scienza sociale. Nel 1642, mentre era ancora un adolescente, iniziò un lavoro pionieristico sul calcolo del mac
 Panoramica della tigre esperimento al triumf acceleratore di particelle laboratorio Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/panoramica-della-tigre-esperimento-al-triumf-acceleratore-di-particelle-laboratorio-image66744835.html
Panoramica della tigre esperimento al triumf acceleratore di particelle laboratorio Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/panoramica-della-tigre-esperimento-al-triumf-acceleratore-di-particelle-laboratorio-image66744835.htmlRMDTGDM3–Panoramica della tigre esperimento al triumf acceleratore di particelle laboratorio
 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184260.html
'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184260.htmlRMGPJ5M4–'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
 Due viste del disegno perpettivo, 18° C. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/due-viste-del-disegno-perpettivo-18-c-image352803529.html
Due viste del disegno perpettivo, 18° C. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/due-viste-del-disegno-perpettivo-18-c-image352803529.htmlRM2BDYGE1–Due viste del disegno perpettivo, 18° C.
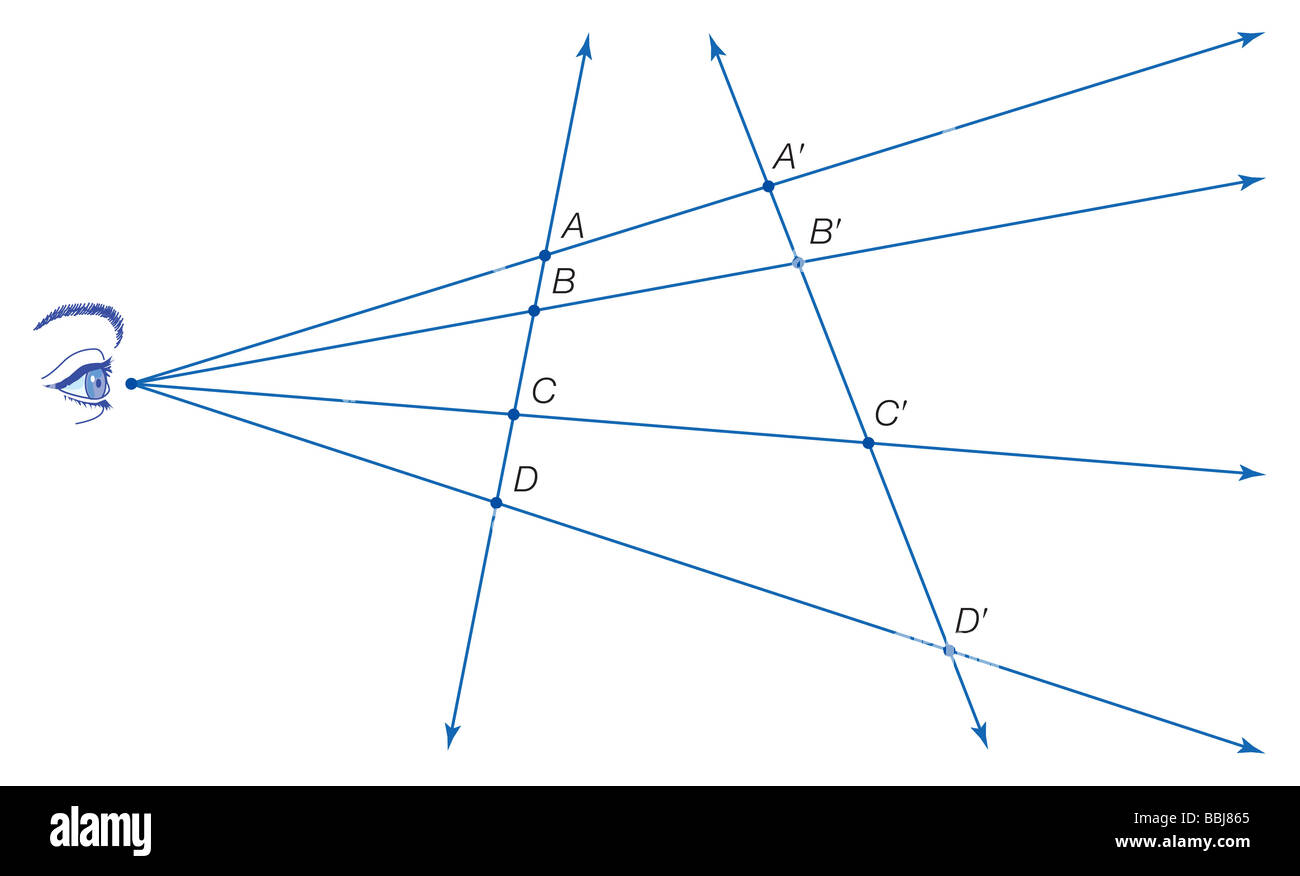 Anche se le distanze e i rapporti di distanze non sono il rapporto di croce, definito come AC/BC · BD/annuncio, è conservato sotto la proiezione. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-anche-se-le-distanze-e-i-rapporti-di-distanze-non-sono-il-rapporto-di-croce-definito-come-ac-bc-bd-annuncio-e-conservato-sotto-la-proiezione-24373165.html
Anche se le distanze e i rapporti di distanze non sono il rapporto di croce, definito come AC/BC · BD/annuncio, è conservato sotto la proiezione. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-anche-se-le-distanze-e-i-rapporti-di-distanze-non-sono-il-rapporto-di-croce-definito-come-ac-bc-bd-annuncio-e-conservato-sotto-la-proiezione-24373165.htmlRMBBJ865–Anche se le distanze e i rapporti di distanze non sono il rapporto di croce, definito come AC/BC · BD/annuncio, è conservato sotto la proiezione.
 Cancun, Messico; Lug 15 2018: rampa circolare di ingresso. Moderno e minimalista struttura in calcestruzzo. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-rampa-circolare-di-ingresso-moderno-e-minimalista-struttura-in-calcestruzzo-image214366281.html
Cancun, Messico; Lug 15 2018: rampa circolare di ingresso. Moderno e minimalista struttura in calcestruzzo. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-rampa-circolare-di-ingresso-moderno-e-minimalista-struttura-in-calcestruzzo-image214366281.htmlRFPCN6AH–Cancun, Messico; Lug 15 2018: rampa circolare di ingresso. Moderno e minimalista struttura in calcestruzzo.
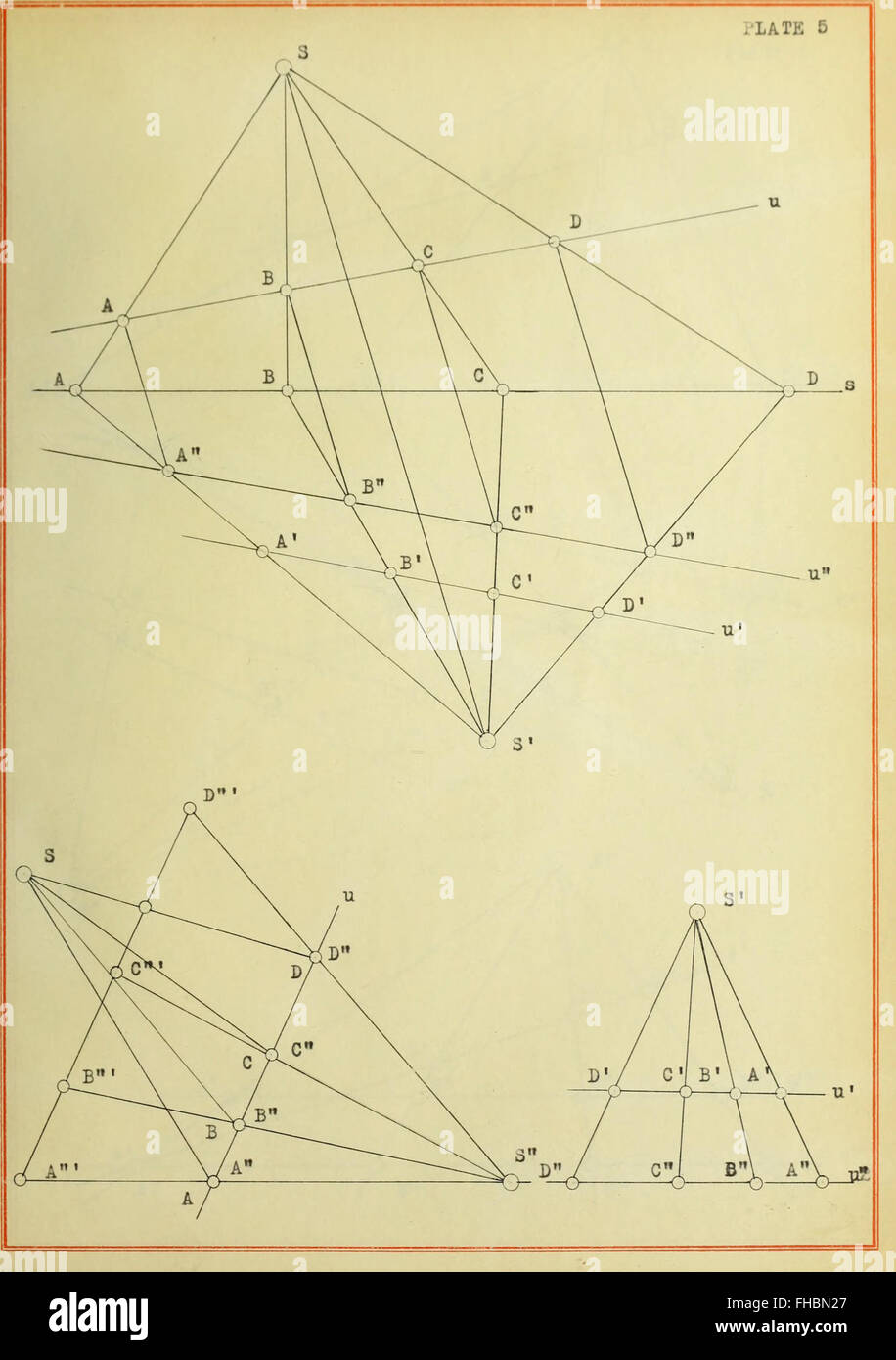 Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-96758991.html
Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-96758991.htmlRMFHBN27–Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915)
 . I principi di geometria proiettiva applicati ai vertici lineari e conici sono A, B, C. poiché A, Bo, C^ sono collineari, byMenelaus Theorem BA 1 CA CB2 AciABo BC Let .1, B, C, .1, B, t sono i vertici dell'esagono e sia A, BB, CCMeet i lati del triangolo ABC INA, B, C. è necessario dimostrare che Thata A, BB, CC sono concorrenti. Lasciate che le tangenti da A, B, C maetthe lati del triangolo ABC in AIA^,B1B2, C1C2 come nella figura. Poiché A, BB^, CC2 sono concorrenti, da Cevas Theorem ^ 1CA CBT^ AB, UN CO1 BC2 * se la linea LM incontra il cerchio in punti reali iu il primo caso o Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/i-principi-di-geometria-proiettiva-applicati-ai-vertici-lineari-e-conici-sono-a-b-c-poiche-a-bo-c-sono-collineari-bymenelaus-theorem-ba-1-ca-cb2-aciabo-bc-let-1-b-c-1-b-t-sono-i-vertici-dell-esagono-e-sia-a-bb-ccmeet-i-lati-del-triangolo-abc-ina-b-c-e-necessario-dimostrare-che-thata-a-bb-cc-sono-concorrenti-lasciate-che-le-tangenti-da-a-b-c-maetthe-lati-del-triangolo-abc-in-aia-b1b2-c1c2-come-nella-figura-poiche-a-bb-cc2-sono-concorrenti-da-cevas-theorem-1ca-cbt-ab-un-co1-bc2-se-la-linea-lm-incontra-il-cerchio-in-punti-reali-iu-il-primo-caso-o-image372410661.html
. I principi di geometria proiettiva applicati ai vertici lineari e conici sono A, B, C. poiché A, Bo, C^ sono collineari, byMenelaus Theorem BA 1 CA CB2 AciABo BC Let .1, B, C, .1, B, t sono i vertici dell'esagono e sia A, BB, CCMeet i lati del triangolo ABC INA, B, C. è necessario dimostrare che Thata A, BB, CC sono concorrenti. Lasciate che le tangenti da A, B, C maetthe lati del triangolo ABC in AIA^,B1B2, C1C2 come nella figura. Poiché A, BB^, CC2 sono concorrenti, da Cevas Theorem ^ 1CA CBT^ AB, UN CO1 BC2 * se la linea LM incontra il cerchio in punti reali iu il primo caso o Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/i-principi-di-geometria-proiettiva-applicati-ai-vertici-lineari-e-conici-sono-a-b-c-poiche-a-bo-c-sono-collineari-bymenelaus-theorem-ba-1-ca-cb2-aciabo-bc-let-1-b-c-1-b-t-sono-i-vertici-dell-esagono-e-sia-a-bb-ccmeet-i-lati-del-triangolo-abc-ina-b-c-e-necessario-dimostrare-che-thata-a-bb-cc-sono-concorrenti-lasciate-che-le-tangenti-da-a-b-c-maetthe-lati-del-triangolo-abc-in-aia-b1b2-c1c2-come-nella-figura-poiche-a-bb-cc2-sono-concorrenti-da-cevas-theorem-1ca-cbt-ab-un-co1-bc2-se-la-linea-lm-incontra-il-cerchio-in-punti-reali-iu-il-primo-caso-o-image372410661.htmlRM2CHTNGN–. I principi di geometria proiettiva applicati ai vertici lineari e conici sono A, B, C. poiché A, Bo, C^ sono collineari, byMenelaus Theorem BA 1 CA CB2 AciABo BC Let .1, B, C, .1, B, t sono i vertici dell'esagono e sia A, BB, CCMeet i lati del triangolo ABC INA, B, C. è necessario dimostrare che Thata A, BB, CC sono concorrenti. Lasciate che le tangenti da A, B, C maetthe lati del triangolo ABC in AIA^,B1B2, C1C2 come nella figura. Poiché A, BB^, CC2 sono concorrenti, da Cevas Theorem ^ 1CA CBT^ AB, UN CO1 BC2 * se la linea LM incontra il cerchio in punti reali iu il primo caso o
 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184272.html
'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184272.htmlRMGPJ5MG–'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
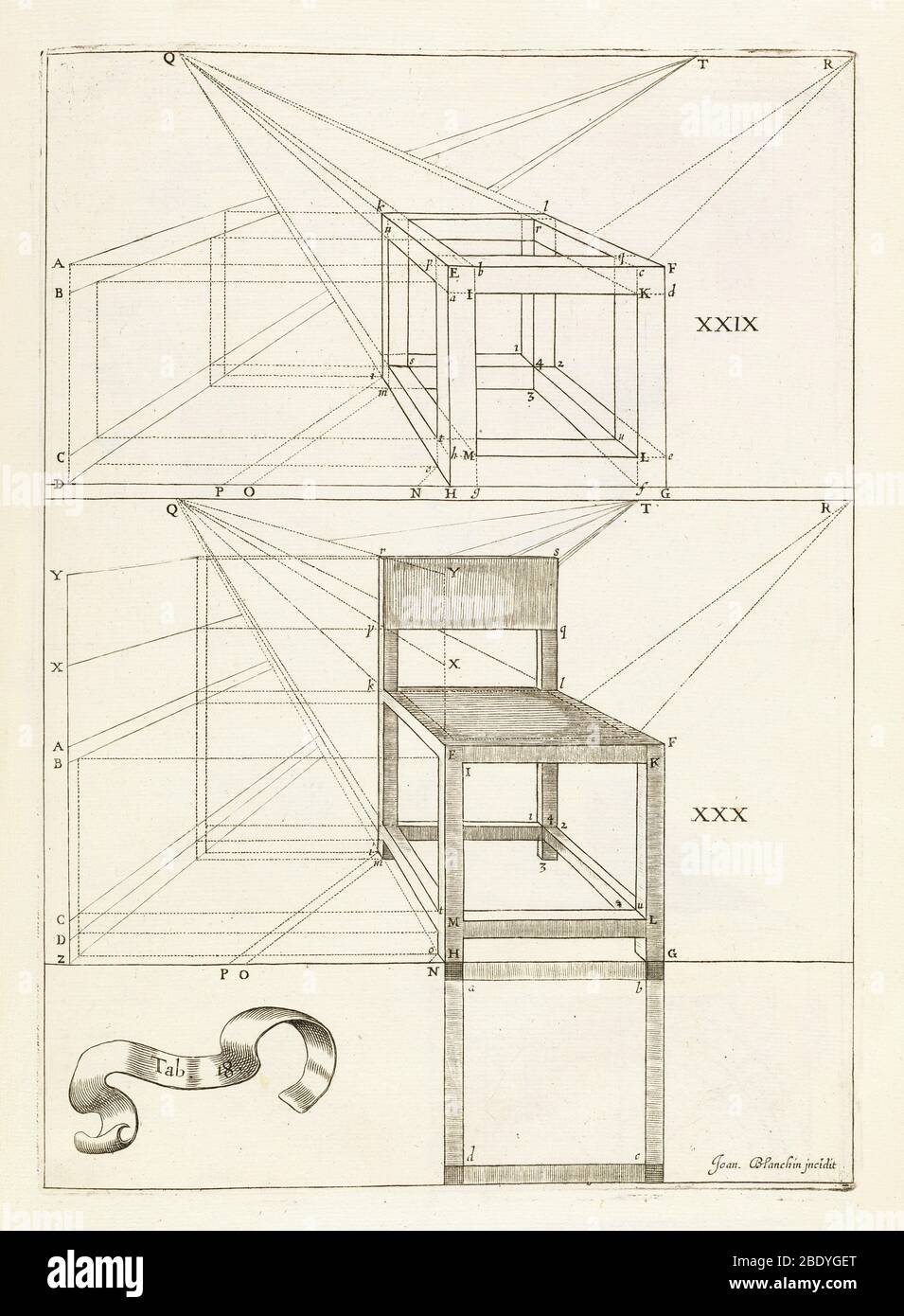 Prospettiva di una sedia, 1652 Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/prospettiva-di-una-sedia-1652-image352803552.html
Prospettiva di una sedia, 1652 Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/prospettiva-di-una-sedia-1652-image352803552.htmlRM2BDYGET–Prospettiva di una sedia, 1652
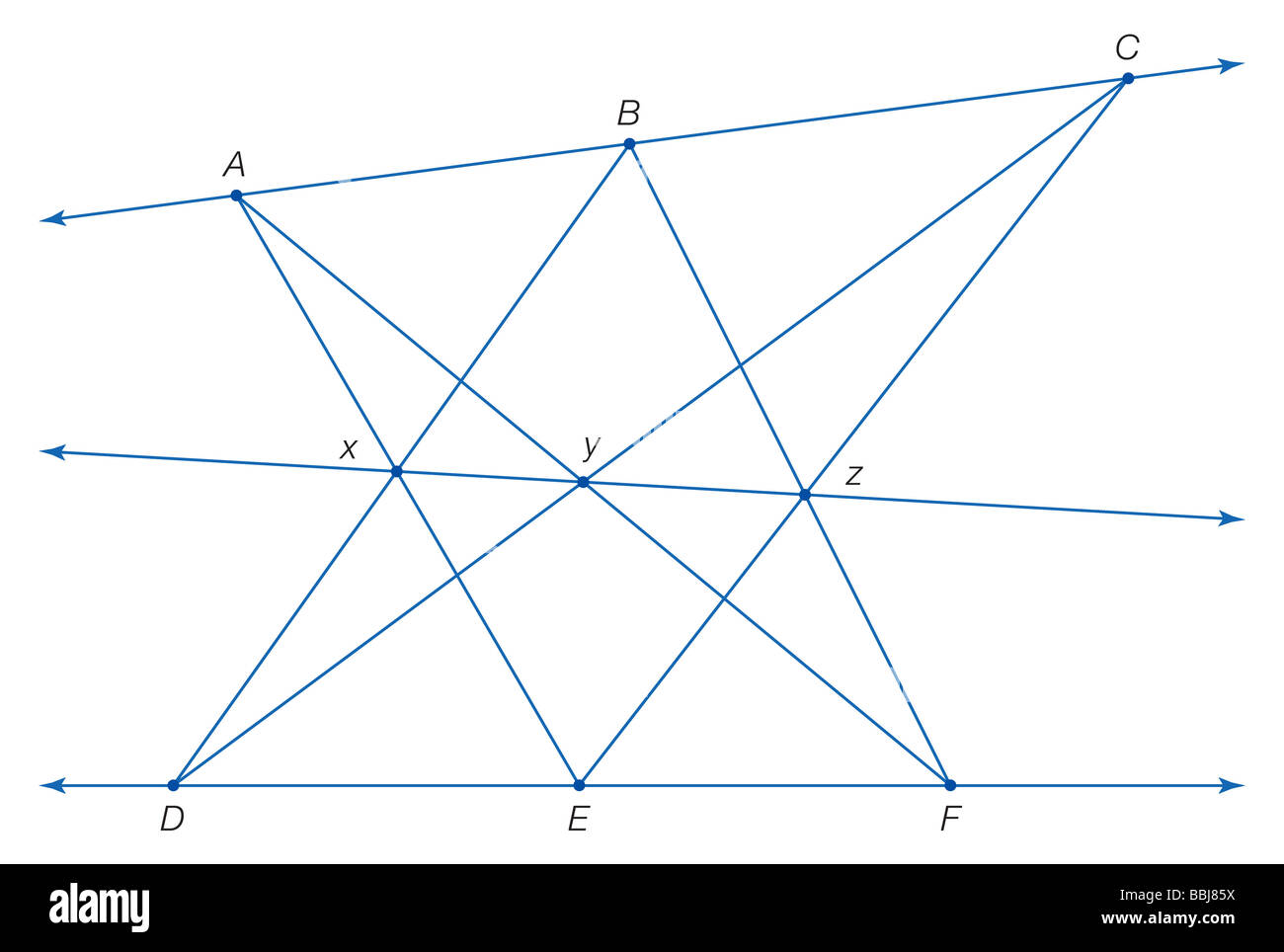 Pappus di Alessandria si è dimostrato che i 3 punti formata da 6 linee di collegamento 2 set di punti collineari sono collineari. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-pappus-di-alessandria-si-e-dimostrato-che-i-3-punti-formata-da-6-linee-di-collegamento-2-set-di-punti-collineari-sono-collineari-24373158.html
Pappus di Alessandria si è dimostrato che i 3 punti formata da 6 linee di collegamento 2 set di punti collineari sono collineari. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-pappus-di-alessandria-si-e-dimostrato-che-i-3-punti-formata-da-6-linee-di-collegamento-2-set-di-punti-collineari-sono-collineari-24373158.htmlRMBBJ85X–Pappus di Alessandria si è dimostrato che i 3 punti formata da 6 linee di collegamento 2 set di punti collineari sono collineari.
 Cancun, Messico; Lug 15 2018: metallo ringhiera bianca con alcuni sport arrugginito. punto di fuga di linee rette dirigere lo sguardo Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-metallo-ringhiera-bianca-con-alcuni-sport-arrugginito-punto-di-fuga-di-linee-rette-dirigere-lo-sguardo-image214366305.html
Cancun, Messico; Lug 15 2018: metallo ringhiera bianca con alcuni sport arrugginito. punto di fuga di linee rette dirigere lo sguardo Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-metallo-ringhiera-bianca-con-alcuni-sport-arrugginito-punto-di-fuga-di-linee-rette-dirigere-lo-sguardo-image214366305.htmlRFPCN6BD–Cancun, Messico; Lug 15 2018: metallo ringhiera bianca con alcuni sport arrugginito. punto di fuga di linee rette dirigere lo sguardo
 Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-96758995.html
Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-96758995.htmlRMFHBN2B–Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915)
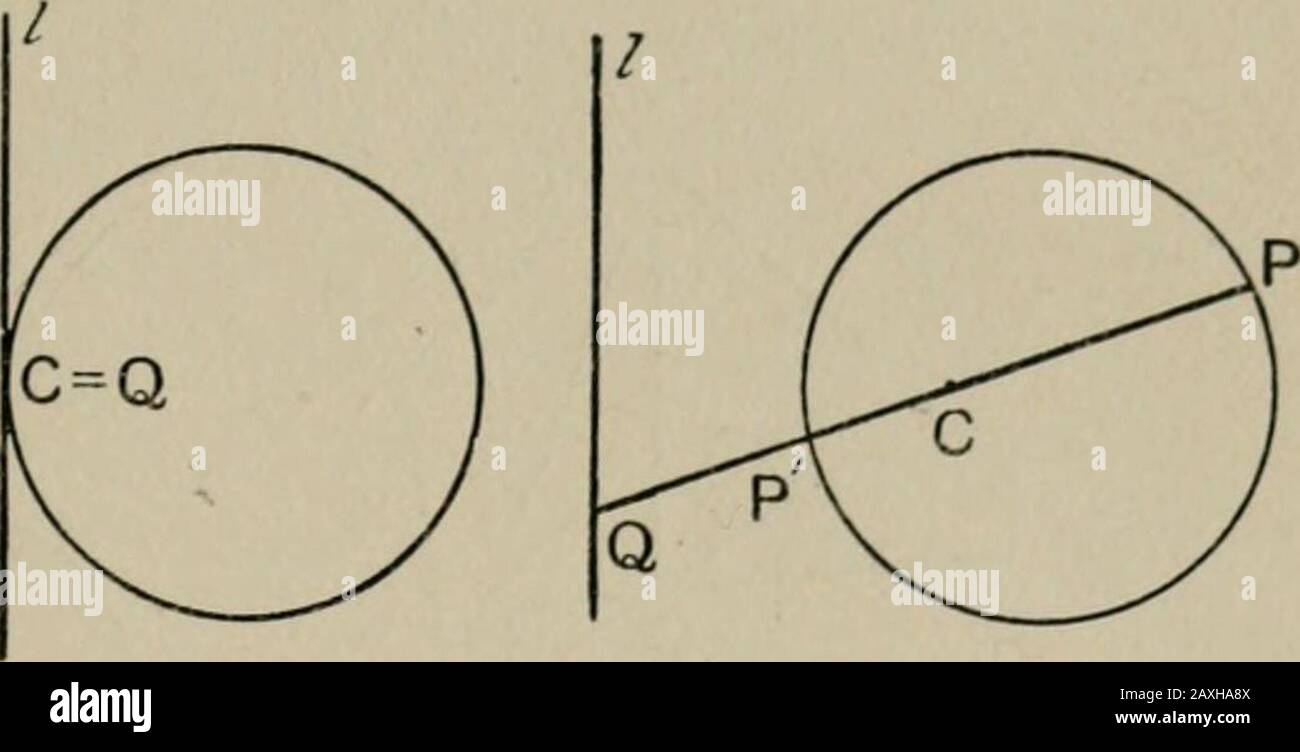 Un primo corso nella geometria proiettiva . Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-image343359322.html
Un primo corso nella geometria proiettiva . Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-image343359322.htmlRM2AXHA8X–Un primo corso nella geometria proiettiva .
 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184247.html
'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184247.htmlRMGPJ5KK–'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
 Profilo di una figura utilizzando uno strumento geometrico, eventualmente che mostra la misura utilizzando la vista prospettica di un gruppo di alberi. Incisione da 'Utriusque cosmi' di Robert Fludd, 1618. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/profilo-di-una-figura-utilizzando-uno-strumento-geometrico-eventualmente-che-mostra-la-misura-utilizzando-la-vista-prospettica-di-un-gruppo-di-alberi-incisione-da-utriusque-cosmi-di-robert-fludd-1618-image246624810.html
Profilo di una figura utilizzando uno strumento geometrico, eventualmente che mostra la misura utilizzando la vista prospettica di un gruppo di alberi. Incisione da 'Utriusque cosmi' di Robert Fludd, 1618. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/profilo-di-una-figura-utilizzando-uno-strumento-geometrico-eventualmente-che-mostra-la-misura-utilizzando-la-vista-prospettica-di-un-gruppo-di-alberi-incisione-da-utriusque-cosmi-di-robert-fludd-1618-image246624810.htmlRMT96MCX–Profilo di una figura utilizzando uno strumento geometrico, eventualmente che mostra la misura utilizzando la vista prospettica di un gruppo di alberi. Incisione da 'Utriusque cosmi' di Robert Fludd, 1618.
 Le sezioni coniche possono essere generate proiettando il cerchio formato dall'intersezione di un cono con la realtà piano perpend Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-le-sezioni-coniche-possono-essere-generate-proiettando-il-cerchio-formato-dall-intersezione-di-un-cono-con-la-realta-piano-perpend-24373169.html
Le sezioni coniche possono essere generate proiettando il cerchio formato dall'intersezione di un cono con la realtà piano perpend Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-le-sezioni-coniche-possono-essere-generate-proiettando-il-cerchio-formato-dall-intersezione-di-un-cono-con-la-realta-piano-perpend-24373169.htmlRMBBJ869–Le sezioni coniche possono essere generate proiettando il cerchio formato dall'intersezione di un cono con la realtà piano perpend
 Cancun, Messico; Lug 15 2018: rampa circolare di ingresso. Moderno e minimalista struttura in calcestruzzo. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-rampa-circolare-di-ingresso-moderno-e-minimalista-struttura-in-calcestruzzo-image214366275.html
Cancun, Messico; Lug 15 2018: rampa circolare di ingresso. Moderno e minimalista struttura in calcestruzzo. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-rampa-circolare-di-ingresso-moderno-e-minimalista-struttura-in-calcestruzzo-image214366275.htmlRFPCN6AB–Cancun, Messico; Lug 15 2018: rampa circolare di ingresso. Moderno e minimalista struttura in calcestruzzo.
 Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-96758993.html
Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-96758993.htmlRMFHBN29–Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915)
 Origine e sviluppo del teorema fondamentale della geometria proiettiva . Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-image339205339.html
Origine e sviluppo del teorema fondamentale della geometria proiettiva . Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-image339205339.htmlRM2AKT3TB–Origine e sviluppo del teorema fondamentale della geometria proiettiva .
 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184242.html
'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184242.htmlRMGPJ5KE–'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
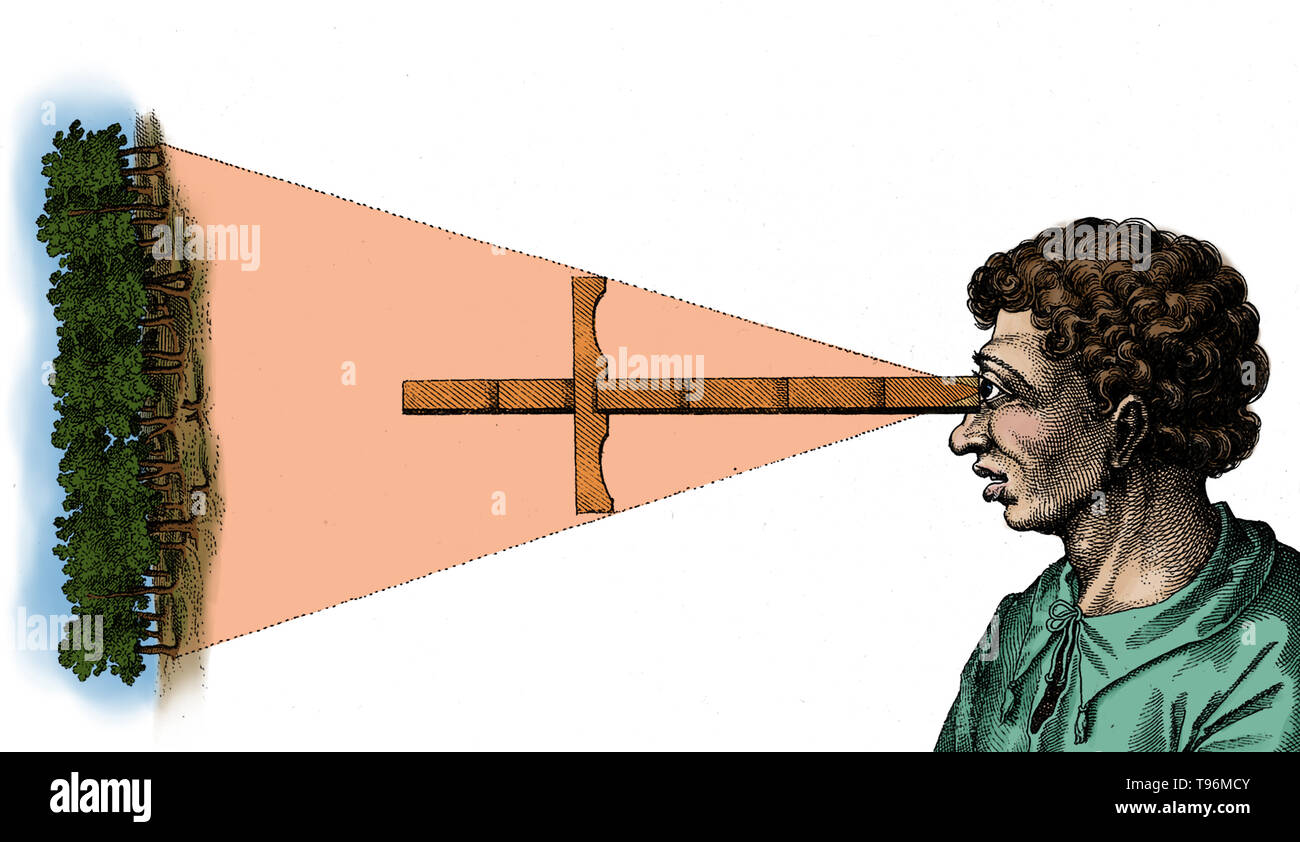 Profilo di una figura utilizzando uno strumento geometrico, eventualmente che mostra la misura utilizzando la vista prospettica di un gruppo di alberi. Incisione da 'Utriusque cosmi' di Robert Fludd, 1618. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/profilo-di-una-figura-utilizzando-uno-strumento-geometrico-eventualmente-che-mostra-la-misura-utilizzando-la-vista-prospettica-di-un-gruppo-di-alberi-incisione-da-utriusque-cosmi-di-robert-fludd-1618-image246624811.html
Profilo di una figura utilizzando uno strumento geometrico, eventualmente che mostra la misura utilizzando la vista prospettica di un gruppo di alberi. Incisione da 'Utriusque cosmi' di Robert Fludd, 1618. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/profilo-di-una-figura-utilizzando-uno-strumento-geometrico-eventualmente-che-mostra-la-misura-utilizzando-la-vista-prospettica-di-un-gruppo-di-alberi-incisione-da-utriusque-cosmi-di-robert-fludd-1618-image246624811.htmlRMT96MCY–Profilo di una figura utilizzando uno strumento geometrico, eventualmente che mostra la misura utilizzando la vista prospettica di un gruppo di alberi. Incisione da 'Utriusque cosmi' di Robert Fludd, 1618.
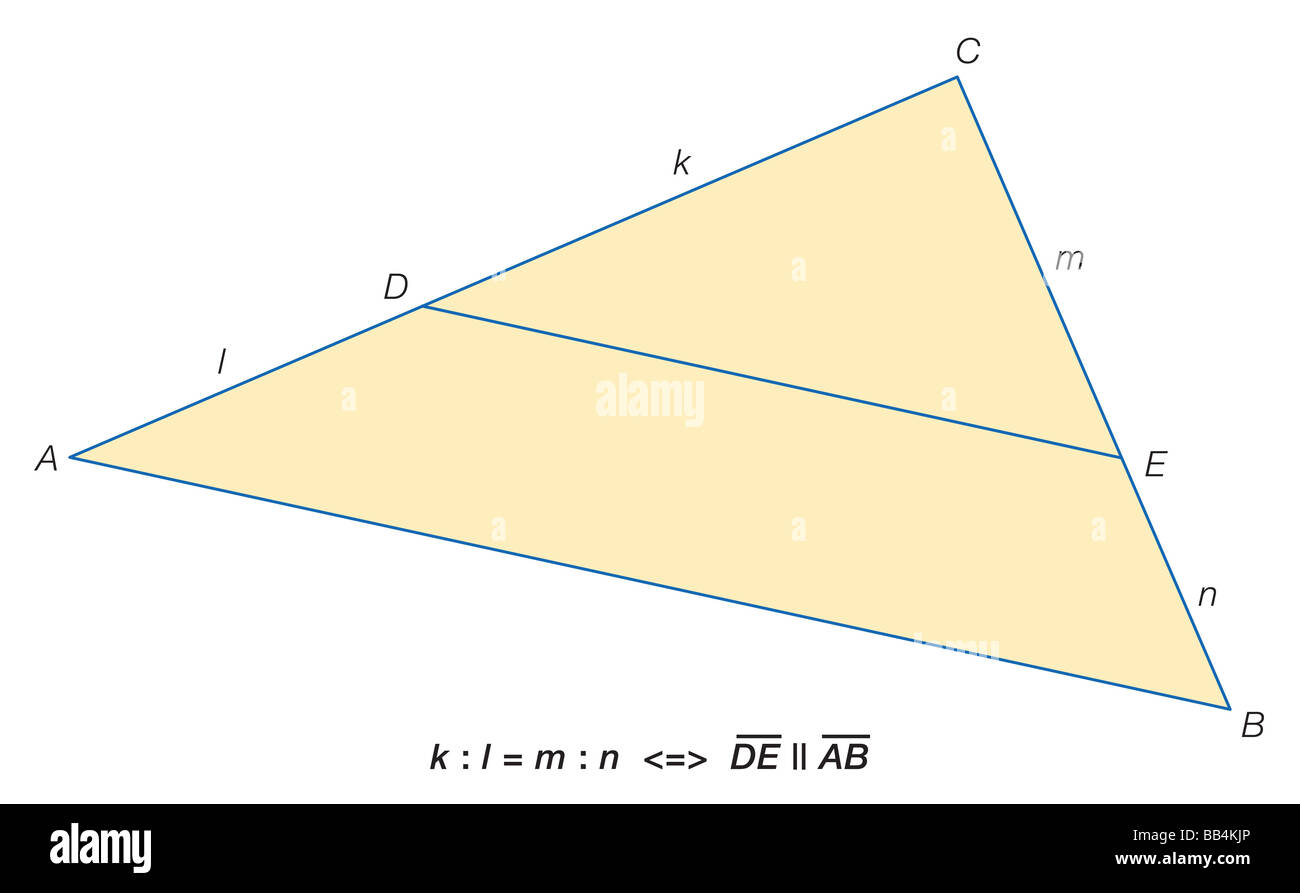 Una dimostrazione del teorema fondamentale di somiglianza, mostra che le piccole e grandi triangoli sono simili. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-una-dimostrazione-del-teorema-fondamentale-di-somiglianza-mostra-che-le-piccole-e-grandi-triangoli-sono-simili-24074814.html
Una dimostrazione del teorema fondamentale di somiglianza, mostra che le piccole e grandi triangoli sono simili. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-una-dimostrazione-del-teorema-fondamentale-di-somiglianza-mostra-che-le-piccole-e-grandi-triangoli-sono-simili-24074814.htmlRMBB4KJP–Una dimostrazione del teorema fondamentale di somiglianza, mostra che le piccole e grandi triangoli sono simili.
 Cancun, Messico; Lug 15 2018: metallo ringhiera bianca con alcuni sport arrugginito. punto di fuga di linee rette dirigere lo sguardo Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-metallo-ringhiera-bianca-con-alcuni-sport-arrugginito-punto-di-fuga-di-linee-rette-dirigere-lo-sguardo-image214366294.html
Cancun, Messico; Lug 15 2018: metallo ringhiera bianca con alcuni sport arrugginito. punto di fuga di linee rette dirigere lo sguardo Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-metallo-ringhiera-bianca-con-alcuni-sport-arrugginito-punto-di-fuga-di-linee-rette-dirigere-lo-sguardo-image214366294.htmlRFPCN6B2–Cancun, Messico; Lug 15 2018: metallo ringhiera bianca con alcuni sport arrugginito. punto di fuga di linee rette dirigere lo sguardo
 Una incisione di Albrecht Dürer (1478-1528), "dimostrazione del disegno in prospettiva di un liuto' (1525). Questa xilografia è preso da un trattato di Dürer ha scritto sull'applicazione della geometria di arte. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-una-incisione-di-albrecht-durer-1478-1528-dimostrazione-del-disegno-in-prospettiva-di-un-liuto-1525-questa-xilografia-e-preso-da-un-trattato-di-durer-ha-scritto-sull-applicazione-della-geometria-di-arte-103999704.html
Una incisione di Albrecht Dürer (1478-1528), "dimostrazione del disegno in prospettiva di un liuto' (1525). Questa xilografia è preso da un trattato di Dürer ha scritto sull'applicazione della geometria di arte. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-una-incisione-di-albrecht-durer-1478-1528-dimostrazione-del-disegno-in-prospettiva-di-un-liuto-1525-questa-xilografia-e-preso-da-un-trattato-di-durer-ha-scritto-sull-applicazione-della-geometria-di-arte-103999704.htmlRMG15GK4–Una incisione di Albrecht Dürer (1478-1528), "dimostrazione del disegno in prospettiva di un liuto' (1525). Questa xilografia è preso da un trattato di Dürer ha scritto sull'applicazione della geometria di arte.
 Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-87033144.html
Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-87033144.htmlRMF1GKJG–Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915)
 Origine e sviluppo del teorema fondamentale della geometria proiettiva . Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-image339206398.html
Origine e sviluppo del teorema fondamentale della geometria proiettiva . Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-image339206398.htmlRM2AKT566–Origine e sviluppo del teorema fondamentale della geometria proiettiva .
 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184237.html
'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184237.htmlRMGPJ5K9–'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
 Per qualsiasi esagono in qualsiasi sezione conica le tre coppie di lati opposti si intersecano in punti su una linea retta quando esteso. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-per-qualsiasi-esagono-in-qualsiasi-sezione-conica-le-tre-coppie-di-lati-opposti-si-intersecano-in-punti-su-una-linea-retta-quando-esteso-24074558.html
Per qualsiasi esagono in qualsiasi sezione conica le tre coppie di lati opposti si intersecano in punti su una linea retta quando esteso. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-per-qualsiasi-esagono-in-qualsiasi-sezione-conica-le-tre-coppie-di-lati-opposti-si-intersecano-in-punti-su-una-linea-retta-quando-esteso-24074558.htmlRMBB4K9J–Per qualsiasi esagono in qualsiasi sezione conica le tre coppie di lati opposti si intersecano in punti su una linea retta quando esteso.
 Cancun, Messico; Lug 15 2018: metallo ringhiera bianca con alcuni sport arrugginito. punto di fuga di linee rette dirigere lo sguardo Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-metallo-ringhiera-bianca-con-alcuni-sport-arrugginito-punto-di-fuga-di-linee-rette-dirigere-lo-sguardo-image214366325.html
Cancun, Messico; Lug 15 2018: metallo ringhiera bianca con alcuni sport arrugginito. punto di fuga di linee rette dirigere lo sguardo Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-metallo-ringhiera-bianca-con-alcuni-sport-arrugginito-punto-di-fuga-di-linee-rette-dirigere-lo-sguardo-image214366325.htmlRFPCN6C5–Cancun, Messico; Lug 15 2018: metallo ringhiera bianca con alcuni sport arrugginito. punto di fuga di linee rette dirigere lo sguardo
 Vista griglia per disegno del XVI secolo Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/vista-griglia-per-disegno-del-xvi-secolo-image151887902.html
Vista griglia per disegno del XVI secolo Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/vista-griglia-per-disegno-del-xvi-secolo-image151887902.htmlRMJR32FX–Vista griglia per disegno del XVI secolo
 Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-87033145.html
Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-87033145.htmlRMF1GKJH–Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915)
 Origine e sviluppo del teorema fondamentale della geometria proiettiva . ?Fine 8 Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-fine-8-image339204310.html
Origine e sviluppo del teorema fondamentale della geometria proiettiva . ?Fine 8 Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-fine-8-image339204310.htmlRM2AKT2FJ–Origine e sviluppo del teorema fondamentale della geometria proiettiva . ?Fine 8
 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184250.html
'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184250.htmlRMGPJ5KP–'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
 L'occhio si connette a punti sul piano della realtà attraverso la vista delle linee che si intersecano con il piano immagine, generando il disegno. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-l-occhio-si-connette-a-punti-sul-piano-della-realta-attraverso-la-vista-delle-linee-che-si-intersecano-con-il-piano-immagine-generando-il-disegno-24373148.html
L'occhio si connette a punti sul piano della realtà attraverso la vista delle linee che si intersecano con il piano immagine, generando il disegno. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-l-occhio-si-connette-a-punti-sul-piano-della-realta-attraverso-la-vista-delle-linee-che-si-intersecano-con-il-piano-immagine-generando-il-disegno-24373148.htmlRMBBJ85G–L'occhio si connette a punti sul piano della realtà attraverso la vista delle linee che si intersecano con il piano immagine, generando il disegno.
 Cancun, Messico; Lug 15 2018: metallo ringhiera bianca con alcuni sport arrugginito. punto di fuga di linee rette dirigere lo sguardo Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-metallo-ringhiera-bianca-con-alcuni-sport-arrugginito-punto-di-fuga-di-linee-rette-dirigere-lo-sguardo-image214366288.html
Cancun, Messico; Lug 15 2018: metallo ringhiera bianca con alcuni sport arrugginito. punto di fuga di linee rette dirigere lo sguardo Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-metallo-ringhiera-bianca-con-alcuni-sport-arrugginito-punto-di-fuga-di-linee-rette-dirigere-lo-sguardo-image214366288.htmlRFPCN6AT–Cancun, Messico; Lug 15 2018: metallo ringhiera bianca con alcuni sport arrugginito. punto di fuga di linee rette dirigere lo sguardo
 Diagramma di prospettiva,1521 Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/diagramma-di-prospettiva-1521-image151887901.html
Diagramma di prospettiva,1521 Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/diagramma-di-prospettiva-1521-image151887901.htmlRMJR32FW–Diagramma di prospettiva,1521
 Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-87033147.html
Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-1915-87033147.htmlRMF1GKJK–Origine e sviluppo del teorema fondamentale della geometria proiettiva (1915)
 Un primo corso nella geometria proiettiva . 28845I N F UNIVERSITÀ DELLA CALIFORNIA UB:RARY Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-28845i-n-f-universita-della-california-ub-rary-image343333287.html
Un primo corso nella geometria proiettiva . 28845I N F UNIVERSITÀ DELLA CALIFORNIA UB:RARY Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-28845i-n-f-universita-della-california-ub-rary-image343333287.htmlRM2AXG533–Un primo corso nella geometria proiettiva . 28845I N F UNIVERSITÀ DELLA CALIFORNIA UB:RARY
 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184256.html
'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184256.htmlRMGPJ5M0–'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
 Pascal ha dimostrato che i 3 punti formata mediante intersezione delle 6 linee che collegano ogni 6 punti distinti su un cerchio sono collineari. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-pascal-ha-dimostrato-che-i-3-punti-formata-mediante-intersezione-delle-6-linee-che-collegano-ogni-6-punti-distinti-su-un-cerchio-sono-collineari-24373162.html
Pascal ha dimostrato che i 3 punti formata mediante intersezione delle 6 linee che collegano ogni 6 punti distinti su un cerchio sono collineari. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-pascal-ha-dimostrato-che-i-3-punti-formata-mediante-intersezione-delle-6-linee-che-collegano-ogni-6-punti-distinti-su-un-cerchio-sono-collineari-24373162.htmlRMBBJ862–Pascal ha dimostrato che i 3 punti formata mediante intersezione delle 6 linee che collegano ogni 6 punti distinti su un cerchio sono collineari.
 Cancun, Messico; Lug 15 2018: rampa circolare di ingresso. Moderno e minimalista struttura in calcestruzzo. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-rampa-circolare-di-ingresso-moderno-e-minimalista-struttura-in-calcestruzzo-image214366264.html
Cancun, Messico; Lug 15 2018: rampa circolare di ingresso. Moderno e minimalista struttura in calcestruzzo. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/cancun-messico-lug-15-2018-rampa-circolare-di-ingresso-moderno-e-minimalista-struttura-in-calcestruzzo-image214366264.htmlRFPCN6A0–Cancun, Messico; Lug 15 2018: rampa circolare di ingresso. Moderno e minimalista struttura in calcestruzzo.
 Linee di prospettiva per pittura,1624 Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/linee-di-prospettiva-per-pittura-1624-image151887900.html
Linee di prospettiva per pittura,1624 Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/linee-di-prospettiva-per-pittura-1624-image151887900.htmlRMJR32FT–Linee di prospettiva per pittura,1624
 Un primo corso di Geometria proiettiva (1913) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-un-primo-corso-di-geometria-proiettiva-1913-100349461.html
Un primo corso di Geometria proiettiva (1913) Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-un-primo-corso-di-geometria-proiettiva-1913-100349461.htmlRMFR78N9–Un primo corso di Geometria proiettiva (1913)
 Un primo corso nella geometria proiettiva . :. Dal Cap. XII § 9, d e dmust coincidono. Fig. 102a. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-dal-cap-xii-9-d-e-dmust-coincidono-fig-102a-image343343500.html
Un primo corso nella geometria proiettiva . :. Dal Cap. XII § 9, d e dmust coincidono. Fig. 102a. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-dal-cap-xii-9-d-e-dmust-coincidono-fig-102a-image343343500.htmlRM2AXGJ3T–Un primo corso nella geometria proiettiva . :. Dal Cap. XII § 9, d e dmust coincidono. Fig. 102a.
 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184278.html
'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184278.htmlRMGPJ5MP–'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
 La dualità associa al punto P della linea RS, e viceversa. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-la-dualita-associa-al-punto-p-della-linea-rs-e-viceversa-24899304.html
La dualità associa al punto P della linea RS, e viceversa. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-la-dualita-associa-al-punto-p-della-linea-rs-e-viceversa-24899304.htmlRMBCE78T–La dualità associa al punto P della linea RS, e viceversa.
 DÌ rer il disegno in prospettiva di un liuto Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-di-rer-il-disegno-in-prospettiva-di-un-liuto-135045127.html
DÌ rer il disegno in prospettiva di un liuto Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-di-rer-il-disegno-in-prospettiva-di-un-liuto-135045127.htmlRMHRKRC7–DÌ rer il disegno in prospettiva di un liuto
 Un primo corso nella geometria proiettiva . General Library University of California Berkeley -^MN Dept. LD 21-100m-6,56(B9311sl0)476 General Library University of California Berkeley Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-general-library-university-of-california-berkeley-mn-dept-ld-21-100m-6-56-b9311sl0-476-general-library-university-of-california-berkeley-image343333841.html
Un primo corso nella geometria proiettiva . General Library University of California Berkeley -^MN Dept. LD 21-100m-6,56(B9311sl0)476 General Library University of California Berkeley Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-general-library-university-of-california-berkeley-mn-dept-ld-21-100m-6-56-b9311sl0-476-general-library-university-of-california-berkeley-image343333841.htmlRM2AXG5PW–Un primo corso nella geometria proiettiva . General Library University of California Berkeley -^MN Dept. LD 21-100m-6,56(B9311sl0)476 General Library University of California Berkeley
 Anello di Moebius (striscia) nella zona di topologia di 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-anello-di-moebius-striscia-nella-zona-di-topologia-di-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184221.html
Anello di Moebius (striscia) nella zona di topologia di 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-anello-di-moebius-striscia-nella-zona-di-topologia-di-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184221.htmlRMGPJ5JN–Anello di Moebius (striscia) nella zona di topologia di 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
 Julius Plucker, Fisico tedesco Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-julius-plucker-fisico-tedesco-135090533.html
Julius Plucker, Fisico tedesco Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-julius-plucker-fisico-tedesco-135090533.htmlRMHRNW9W–Julius Plucker, Fisico tedesco
 Un primo corso nella geometria proiettiva . General Library University of California Berkeley -^MN Dept. LD 21-100m-6,56(B9311sl0)476 General Library University of California Berkeley. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-general-library-university-of-california-berkeley-mn-dept-ld-21-100m-6-56-b9311sl0-476-general-library-university-of-california-berkeley-image343333370.html
Un primo corso nella geometria proiettiva . General Library University of California Berkeley -^MN Dept. LD 21-100m-6,56(B9311sl0)476 General Library University of California Berkeley. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-general-library-university-of-california-berkeley-mn-dept-ld-21-100m-6-56-b9311sl0-476-general-library-university-of-california-berkeley-image343333370.htmlRM2AXG562–Un primo corso nella geometria proiettiva . General Library University of California Berkeley -^MN Dept. LD 21-100m-6,56(B9311sl0)476 General Library University of California Berkeley.
 Anello di Moebius (striscia) nella zona di topologia di 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-anello-di-moebius-striscia-nella-zona-di-topologia-di-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184229.html
Anello di Moebius (striscia) nella zona di topologia di 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-anello-di-moebius-striscia-nella-zona-di-topologia-di-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184229.htmlRMGPJ5K1–Anello di Moebius (striscia) nella zona di topologia di 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
 Jean-Victor Poncelet, matematico francese Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-jean-victor-poncelet-matematico-francese-135090538.html
Jean-Victor Poncelet, matematico francese Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-jean-victor-poncelet-matematico-francese-135090538.htmlRMHRNWA2–Jean-Victor Poncelet, matematico francese
 Un primo corso nella geometria proiettiva . 3WED jw, o •tutti. XJCLLLM nFTD Mn/ ? R ^M. REC CIR AGO 5 83 LD2lA-50m-2,7 l(P2001sl0)476-A-32. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-3wed-jw-o-tutti-xjclllm-nftd-mn-r-m-rec-cir-ago-5-83-ld2la-50m-2-7-l-p2001sl0-476-a-32-image343334106.html
Un primo corso nella geometria proiettiva . 3WED jw, o •tutti. XJCLLLM nFTD Mn/ ? R ^M. REC CIR AGO 5 83 LD2lA-50m-2,7 l(P2001sl0)476-A-32. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-3wed-jw-o-tutti-xjclllm-nftd-mn-r-m-rec-cir-ago-5-83-ld2la-50m-2-7-l-p2001sl0-476-a-32-image343334106.htmlRM2AXG64A–Un primo corso nella geometria proiettiva . 3WED jw, o •tutti. XJCLLLM nFTD Mn/ ? R ^M. REC CIR AGO 5 83 LD2lA-50m-2,7 l(P2001sl0)476-A-32.
 Anello di Moebius (striscia) nella zona di topologia di 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-anello-di-moebius-striscia-nella-zona-di-topologia-di-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184214.html
Anello di Moebius (striscia) nella zona di topologia di 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-anello-di-moebius-striscia-nella-zona-di-topologia-di-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184214.htmlRMGPJ5JE–Anello di Moebius (striscia) nella zona di topologia di 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
 Jean-Victor Poncelet, matematico francese Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-jean-victor-poncelet-matematico-francese-135098072.html
Jean-Victor Poncelet, matematico francese Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-jean-victor-poncelet-matematico-francese-135098072.htmlRMHRP6Y4–Jean-Victor Poncelet, matematico francese
 Origine e sviluppo del teorema fondamentale della geometria proiettiva . Fig. 1 A B? EDI. GKC J -o o-o-o- o o o-o o o- una o o ?o- Fig. 3 B o- -o- D 11 esso PJATE 3 A* A B AJ D til > Fino S PLATK. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-fig-1-a-b-edi-gkc-j-o-o-o-o-o-o-o-o-o-o-una-o-o-o-fig-3-b-o-o-d-11-esso-pjate-3-a-a-b-aj-d-til-gt-fino-s-platk-image339207392.html
Origine e sviluppo del teorema fondamentale della geometria proiettiva . Fig. 1 A B? EDI. GKC J -o o-o-o- o o o-o o o- una o o ?o- Fig. 3 B o- -o- D 11 esso PJATE 3 A* A B AJ D til > Fino S PLATK. Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-fig-1-a-b-edi-gkc-j-o-o-o-o-o-o-o-o-o-o-una-o-o-o-fig-3-b-o-o-d-11-esso-pjate-3-a-a-b-aj-d-til-gt-fino-s-platk-image339207392.htmlRM2AKT6DM–Origine e sviluppo del teorema fondamentale della geometria proiettiva . Fig. 1 A B? EDI. GKC J -o o-o-o- o o o-o o o- una o o ?o- Fig. 3 B o- -o- D 11 esso PJATE 3 A* A B AJ D til > Fino S PLATK.
 Anello di Moebius (striscia) nella zona di topologia di 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-anello-di-moebius-striscia-nella-zona-di-topologia-di-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184227.html
Anello di Moebius (striscia) nella zona di topologia di 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-anello-di-moebius-striscia-nella-zona-di-topologia-di-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184227.htmlRMGPJ5JY–Anello di Moebius (striscia) nella zona di topologia di 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
 Jean-Victor Poncelet, matematico francese Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-jean-victor-poncelet-matematico-francese-135098071.html
Jean-Victor Poncelet, matematico francese Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-jean-victor-poncelet-matematico-francese-135098071.htmlRMHRP6Y3–Jean-Victor Poncelet, matematico francese
 Origine e sviluppo del teorema fondamentale della geometria proiettiva . Fig. 2 ILATE 2. Fig. 1 A B? EDI. GKC J -o o-o-o- o o o-o o o- una o o ?o- Fig. 3 B o- -o- D 11 esso PJATE 3 A* A B AJ D til > Fino S PLATK Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-fig-2-ilate-2-fig-1-a-b-edi-gkc-j-o-o-o-o-o-o-o-o-o-o-una-o-o-o-fig-3-b-o-o-d-11-esso-pjate-3-a-a-b-aj-d-til-gt-fino-s-platk-image339208035.html
Origine e sviluppo del teorema fondamentale della geometria proiettiva . Fig. 2 ILATE 2. Fig. 1 A B? EDI. GKC J -o o-o-o- o o o-o o o- una o o ?o- Fig. 3 B o- -o- D 11 esso PJATE 3 A* A B AJ D til > Fino S PLATK Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/origine-e-sviluppo-del-teorema-fondamentale-della-geometria-proiettiva-fig-2-ilate-2-fig-1-a-b-edi-gkc-j-o-o-o-o-o-o-o-o-o-o-una-o-o-o-fig-3-b-o-o-d-11-esso-pjate-3-a-a-b-aj-d-til-gt-fino-s-platk-image339208035.htmlRM2AKT78K–Origine e sviluppo del teorema fondamentale della geometria proiettiva . Fig. 2 ILATE 2. Fig. 1 A B? EDI. GKC J -o o-o-o- o o o-o o o- una o o ?o- Fig. 3 B o- -o- D 11 esso PJATE 3 A* A B AJ D til > Fino S PLATK
 Anello di Moebius (striscia) nella zona di topologia di 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-anello-di-moebius-striscia-nella-zona-di-topologia-di-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184233.html
Anello di Moebius (striscia) nella zona di topologia di 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-anello-di-moebius-striscia-nella-zona-di-topologia-di-mathematica-mostra-permanente-di-matematica-nel-museo-della-scienza-di-boston-stati-uniti-d-america-117184233.htmlRMGPJ5K5–Anello di Moebius (striscia) nella zona di topologia di 'Mathematica' mostra permanente di matematica nel Museo della Scienza di Boston, Stati Uniti d'America
 Girard Desargues, matematico francese Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-girard-desargues-matematico-francese-135042500.html
Girard Desargues, matematico francese Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-girard-desargues-matematico-francese-135042500.htmlRMHRKM2C–Girard Desargues, matematico francese
 Un primo percorso nella geometria proiettiva . e il cui cerchio è la proiezione si trova interamente tra i tangenti nei punti in cui la linea di fuga la taglia e questi tangentspioject negli asintototi. § 16. Alcune proprietà Degli Asintotes. I. si formano con qualsiasi coppia di diametri coniugati matita armonica. Ciò segue immediatamente dal § 7, sezione VI, del presente capitolo, poiché gli asinttoti sono tangenti dal centro. Cor. Gli assi di una conica bisettono gli angoli tra teasintoti. Per essi si tratta di una particolare coppia ortogonale di diametri con-giugati. Quindi il risultato segue da § Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-percorso-nella-geometria-proiettiva-e-il-cui-cerchio-e-la-proiezione-si-trova-interamente-tra-i-tangenti-nei-punti-in-cui-la-linea-di-fuga-la-taglia-e-questi-tangentspioject-negli-asintototi-16-alcune-proprieta-degli-asintotes-i-si-formano-con-qualsiasi-coppia-di-diametri-coniugati-matita-armonica-cio-segue-immediatamente-dal-7-sezione-vi-del-presente-capitolo-poiche-gli-asinttoti-sono-tangenti-dal-centro-cor-gli-assi-di-una-conica-bisettono-gli-angoli-tra-teasintoti-per-essi-si-tratta-di-una-particolare-coppia-ortogonale-di-diametri-con-giugati-quindi-il-risultato-segue-da-image343356039.html
Un primo percorso nella geometria proiettiva . e il cui cerchio è la proiezione si trova interamente tra i tangenti nei punti in cui la linea di fuga la taglia e questi tangentspioject negli asintototi. § 16. Alcune proprietà Degli Asintotes. I. si formano con qualsiasi coppia di diametri coniugati matita armonica. Ciò segue immediatamente dal § 7, sezione VI, del presente capitolo, poiché gli asinttoti sono tangenti dal centro. Cor. Gli assi di una conica bisettono gli angoli tra teasintoti. Per essi si tratta di una particolare coppia ortogonale di diametri con-giugati. Quindi il risultato segue da § Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-percorso-nella-geometria-proiettiva-e-il-cui-cerchio-e-la-proiezione-si-trova-interamente-tra-i-tangenti-nei-punti-in-cui-la-linea-di-fuga-la-taglia-e-questi-tangentspioject-negli-asintototi-16-alcune-proprieta-degli-asintotes-i-si-formano-con-qualsiasi-coppia-di-diametri-coniugati-matita-armonica-cio-segue-immediatamente-dal-7-sezione-vi-del-presente-capitolo-poiche-gli-asinttoti-sono-tangenti-dal-centro-cor-gli-assi-di-una-conica-bisettono-gli-angoli-tra-teasintoti-per-essi-si-tratta-di-una-particolare-coppia-ortogonale-di-diametri-con-giugati-quindi-il-risultato-segue-da-image343356039.htmlRM2AXH63K–Un primo percorso nella geometria proiettiva . e il cui cerchio è la proiezione si trova interamente tra i tangenti nei punti in cui la linea di fuga la taglia e questi tangentspioject negli asintototi. § 16. Alcune proprietà Degli Asintotes. I. si formano con qualsiasi coppia di diametri coniugati matita armonica. Ciò segue immediatamente dal § 7, sezione VI, del presente capitolo, poiché gli asinttoti sono tangenti dal centro. Cor. Gli assi di una conica bisettono gli angoli tra teasintoti. Per essi si tratta di una particolare coppia ortogonale di diametri con-giugati. Quindi il risultato segue da §
 Colore esaltato Ritratto di Blaise Pascal (1623-1662), un matematico francese, fisico, inventore, scrittore, filosofo cattolico e il bambino prodigio. Egli ha reso importanti contributi allo studio dei fluidi, e chiarito i concetti di pressione e di depressione. W Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-colore-esaltato-ritratto-di-blaise-pascal-1623-1662-un-matematico-francese-fisico-inventore-scrittore-filosofo-cattolico-e-il-bambino-prodigio-egli-ha-reso-importanti-contributi-allo-studio-dei-fluidi-e-chiarito-i-concetti-di-pressione-e-di-depressione-w-104002000.html
Colore esaltato Ritratto di Blaise Pascal (1623-1662), un matematico francese, fisico, inventore, scrittore, filosofo cattolico e il bambino prodigio. Egli ha reso importanti contributi allo studio dei fluidi, e chiarito i concetti di pressione e di depressione. W Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-colore-esaltato-ritratto-di-blaise-pascal-1623-1662-un-matematico-francese-fisico-inventore-scrittore-filosofo-cattolico-e-il-bambino-prodigio-egli-ha-reso-importanti-contributi-allo-studio-dei-fluidi-e-chiarito-i-concetti-di-pressione-e-di-depressione-w-104002000.htmlRMG15KH4–Colore esaltato Ritratto di Blaise Pascal (1623-1662), un matematico francese, fisico, inventore, scrittore, filosofo cattolico e il bambino prodigio. Egli ha reso importanti contributi allo studio dei fluidi, e chiarito i concetti di pressione e di depressione. W
 Un primo corso nella geometria proiettiva . a livello ortogonale quando è adiametro. Ma nella parabola la retta a metà strada tra l'apolo e il suo polare e parallelo a quest'ultimo è una tangente (Capitolo VIII § 11, Cor. 2). Da qui le linee che uniscono i punti più temdanti dei lati di un triangolo di aretangents di giugate auto-con alla parabola. Anche il centro del circumcerchio dell'autoconiugatetriangolo è l'ortocentro del triangolo formato dalla congiunzione dei punti centrali dei lati. L'ortocentro del triangolo formato da tre tangenti SI trova sulla direttrice. Es. Dalle proprietà della parabola provare (a Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-a-livello-ortogonale-quando-e-adiametro-ma-nella-parabola-la-retta-a-meta-strada-tra-l-apolo-e-il-suo-polare-e-parallelo-a-quest-ultimo-e-una-tangente-capitolo-viii-11-cor-2-da-qui-le-linee-che-uniscono-i-punti-piu-temdanti-dei-lati-di-un-triangolo-di-aretangents-di-giugate-auto-con-alla-parabola-anche-il-centro-del-circumcerchio-dell-autoconiugatetriangolo-e-l-ortocentro-del-triangolo-formato-dalla-congiunzione-dei-punti-centrali-dei-lati-l-ortocentro-del-triangolo-formato-da-tre-tangenti-si-trova-sulla-direttrice-es-dalle-proprieta-della-parabola-provare-a-image343345740.html
Un primo corso nella geometria proiettiva . a livello ortogonale quando è adiametro. Ma nella parabola la retta a metà strada tra l'apolo e il suo polare e parallelo a quest'ultimo è una tangente (Capitolo VIII § 11, Cor. 2). Da qui le linee che uniscono i punti più temdanti dei lati di un triangolo di aretangents di giugate auto-con alla parabola. Anche il centro del circumcerchio dell'autoconiugatetriangolo è l'ortocentro del triangolo formato dalla congiunzione dei punti centrali dei lati. L'ortocentro del triangolo formato da tre tangenti SI trova sulla direttrice. Es. Dalle proprietà della parabola provare (a Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-a-livello-ortogonale-quando-e-adiametro-ma-nella-parabola-la-retta-a-meta-strada-tra-l-apolo-e-il-suo-polare-e-parallelo-a-quest-ultimo-e-una-tangente-capitolo-viii-11-cor-2-da-qui-le-linee-che-uniscono-i-punti-piu-temdanti-dei-lati-di-un-triangolo-di-aretangents-di-giugate-auto-con-alla-parabola-anche-il-centro-del-circumcerchio-dell-autoconiugatetriangolo-e-l-ortocentro-del-triangolo-formato-dalla-congiunzione-dei-punti-centrali-dei-lati-l-ortocentro-del-triangolo-formato-da-tre-tangenti-si-trova-sulla-direttrice-es-dalle-proprieta-della-parabola-provare-a-image343345740.htmlRM2AXGMYT–Un primo corso nella geometria proiettiva . a livello ortogonale quando è adiametro. Ma nella parabola la retta a metà strada tra l'apolo e il suo polare e parallelo a quest'ultimo è una tangente (Capitolo VIII § 11, Cor. 2). Da qui le linee che uniscono i punti più temdanti dei lati di un triangolo di aretangents di giugate auto-con alla parabola. Anche il centro del circumcerchio dell'autoconiugatetriangolo è l'ortocentro del triangolo formato dalla congiunzione dei punti centrali dei lati. L'ortocentro del triangolo formato da tre tangenti SI trova sulla direttrice. Es. Dalle proprietà della parabola provare (a
 Blaise Pascal, Polymath francese Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-blaise-pascal-polymath-francese-134992206.html
Blaise Pascal, Polymath francese Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/foto-immagine-blaise-pascal-polymath-francese-134992206.htmlRMHRHBX6–Blaise Pascal, Polymath francese
 Un primo corso nella geometria proiettiva . lectinge disposizione dei metodi e dà come risultato la geometria Del Piano con vista alla loro applicazione nella teoria della proiezione. Wenow riprende il trattamento di quest'ultimo dal punto in cui è stato lasciato nel capitolo 11. § 2. Le Linee Vanishing. Abbiamo visto che la proiezione di una linea retta è la sezione di un piano attraverso V, il vertice della proiezione e quella linea con il piano di proiezione. Se questi due piani sono paralleli, tuttavia, il proietto diventa la linea all'infinito sul piano di proiezione. Sia TT il piano della figura e tt il Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-lectinge-disposizione-dei-metodi-e-da-come-risultato-la-geometria-del-piano-con-vista-alla-loro-applicazione-nella-teoria-della-proiezione-wenow-riprende-il-trattamento-di-quest-ultimo-dal-punto-in-cui-e-stato-lasciato-nel-capitolo-11-2-le-linee-vanishing-abbiamo-visto-che-la-proiezione-di-una-linea-retta-e-la-sezione-di-un-piano-attraverso-v-il-vertice-della-proiezione-e-quella-linea-con-il-piano-di-proiezione-se-questi-due-piani-sono-paralleli-tuttavia-il-proietto-diventa-la-linea-all-infinito-sul-piano-di-proiezione-sia-tt-il-piano-della-figura-e-tt-il-image343361919.html
Un primo corso nella geometria proiettiva . lectinge disposizione dei metodi e dà come risultato la geometria Del Piano con vista alla loro applicazione nella teoria della proiezione. Wenow riprende il trattamento di quest'ultimo dal punto in cui è stato lasciato nel capitolo 11. § 2. Le Linee Vanishing. Abbiamo visto che la proiezione di una linea retta è la sezione di un piano attraverso V, il vertice della proiezione e quella linea con il piano di proiezione. Se questi due piani sono paralleli, tuttavia, il proietto diventa la linea all'infinito sul piano di proiezione. Sia TT il piano della figura e tt il Foto Stockhttps://www.alamy.it/image-license-details/?v=1https://www.alamy.it/un-primo-corso-nella-geometria-proiettiva-lectinge-disposizione-dei-metodi-e-da-come-risultato-la-geometria-del-piano-con-vista-alla-loro-applicazione-nella-teoria-della-proiezione-wenow-riprende-il-trattamento-di-quest-ultimo-dal-punto-in-cui-e-stato-lasciato-nel-capitolo-11-2-le-linee-vanishing-abbiamo-visto-che-la-proiezione-di-una-linea-retta-e-la-sezione-di-un-piano-attraverso-v-il-vertice-della-proiezione-e-quella-linea-con-il-piano-di-proiezione-se-questi-due-piani-sono-paralleli-tuttavia-il-proietto-diventa-la-linea-all-infinito-sul-piano-di-proiezione-sia-tt-il-piano-della-figura-e-tt-il-image343361919.htmlRM2AXHDHK–Un primo corso nella geometria proiettiva . lectinge disposizione dei metodi e dà come risultato la geometria Del Piano con vista alla loro applicazione nella teoria della proiezione. Wenow riprende il trattamento di quest'ultimo dal punto in cui è stato lasciato nel capitolo 11. § 2. Le Linee Vanishing. Abbiamo visto che la proiezione di una linea retta è la sezione di un piano attraverso V, il vertice della proiezione e quella linea con il piano di proiezione. Se questi due piani sono paralleli, tuttavia, il proietto diventa la linea all'infinito sul piano di proiezione. Sia TT il piano della figura e tt il
